Learning Diffusion Model from Noisy Measurement using Principled Expectation-Maximization Method

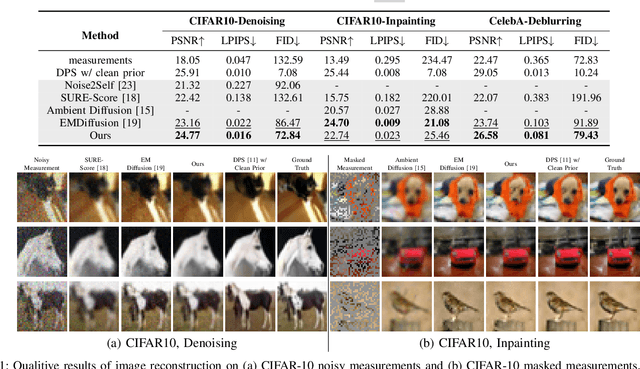
Diffusion models have demonstrated exceptional ability in modeling complex image distributions, making them versatile plug-and-play priors for solving imaging inverse problems. However, their reliance on large-scale clean datasets for training limits their applicability in scenarios where acquiring clean data is costly or impractical. Recent approaches have attempted to learn diffusion models directly from corrupted measurements, but these methods either lack theoretical convergence guarantees or are restricted to specific types of data corruption. In this paper, we propose a principled expectation-maximization (EM) framework that iteratively learns diffusion models from noisy data with arbitrary corruption types. Our framework employs a plug-and-play Monte Carlo method to accurately estimate clean images from noisy measurements, followed by training the diffusion model using the reconstructed images. This process alternates between estimation and training until convergence. We evaluate the performance of our method across various imaging tasks, including inpainting, denoising, and deblurring. Experimental results demonstrate that our approach enables the learning of high-fidelity diffusion priors from noisy data, significantly enhancing reconstruction quality in imaging inverse problems.

Design and Optimization of Hierarchical Gradient Coding for Distributed Learning at Edge Devices

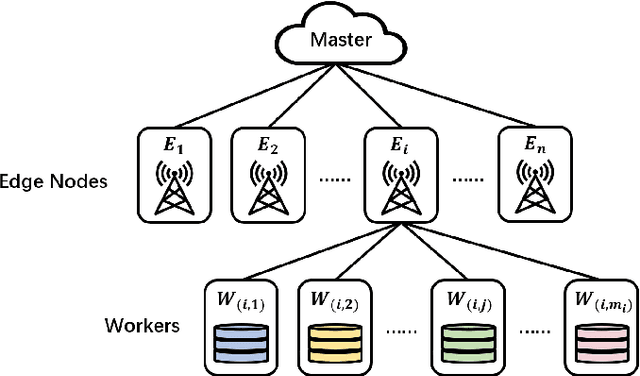
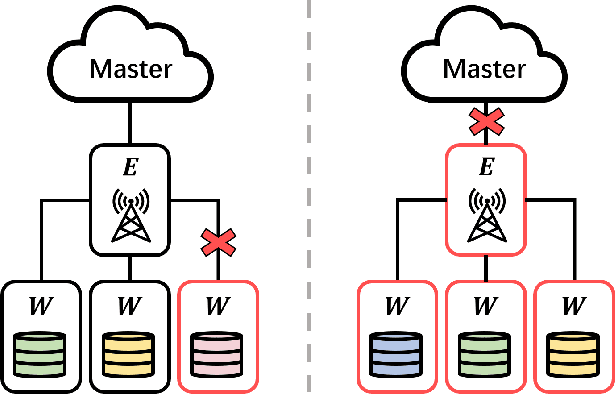
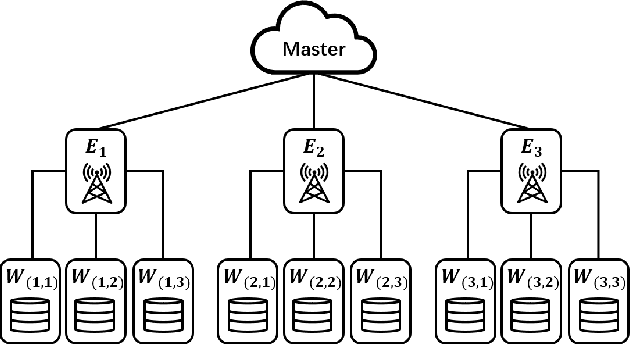
Edge computing has recently emerged as a promising paradigm to boost the performance of distributed learning by leveraging the distributed resources at edge nodes. Architecturally, the introduction of edge nodes adds an additional intermediate layer between the master and workers in the original distributed learning systems, potentially leading to more severe straggler effect. Recently, coding theory-based approaches have been proposed for stragglers mitigation in distributed learning, but the majority focus on the conventional workers-master architecture. In this paper, along a different line, we investigate the problem of mitigating the straggler effect in hierarchical distributed learning systems with an additional layer composed of edge nodes. Technically, we first derive the fundamental trade-off between the computational loads of workers and the stragglers tolerance. Then, we propose a hierarchical gradient coding framework, which provides better stragglers mitigation, to achieve the derived computational trade-off. To further improve the performance of our framework in heterogeneous scenarios, we formulate an optimization problem with the objective of minimizing the expected execution time for each iteration in the learning process. We develop an efficient algorithm to mathematically solve the problem by outputting the optimum strategy. Extensive simulation results demonstrate the superiority of our schemes compared with conventional solutions.