Design and Optimization of Hierarchical Gradient Coding for Distributed Learning at Edge Devices
Paper and Code
Jun 16, 2024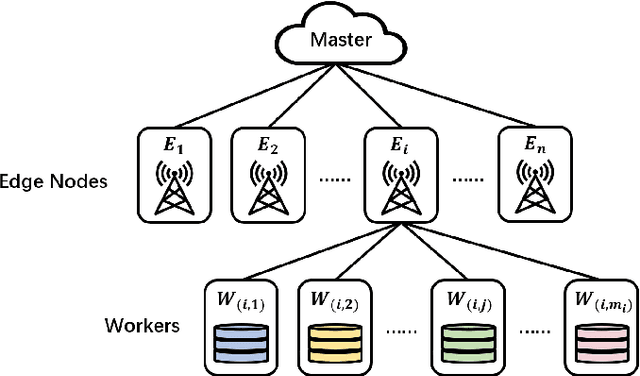
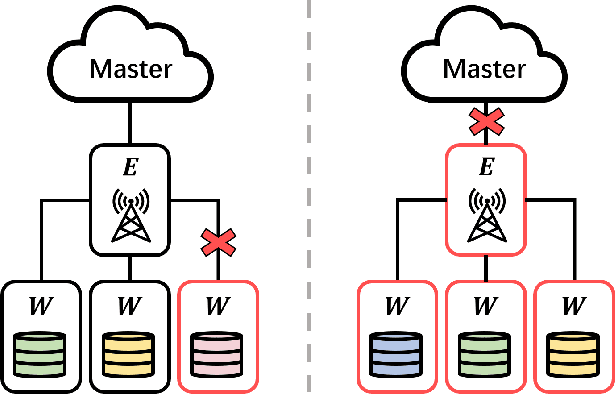
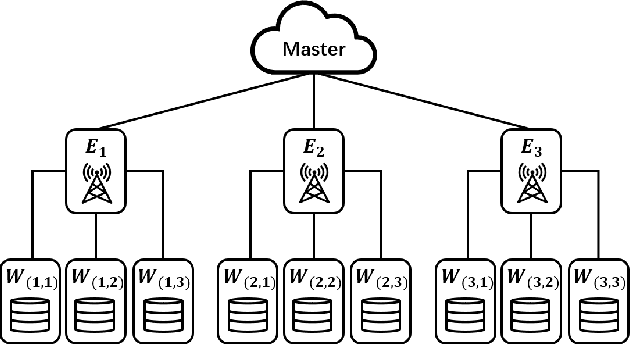

Edge computing has recently emerged as a promising paradigm to boost the performance of distributed learning by leveraging the distributed resources at edge nodes. Architecturally, the introduction of edge nodes adds an additional intermediate layer between the master and workers in the original distributed learning systems, potentially leading to more severe straggler effect. Recently, coding theory-based approaches have been proposed for stragglers mitigation in distributed learning, but the majority focus on the conventional workers-master architecture. In this paper, along a different line, we investigate the problem of mitigating the straggler effect in hierarchical distributed learning systems with an additional layer composed of edge nodes. Technically, we first derive the fundamental trade-off between the computational loads of workers and the stragglers tolerance. Then, we propose a hierarchical gradient coding framework, which provides better stragglers mitigation, to achieve the derived computational trade-off. To further improve the performance of our framework in heterogeneous scenarios, we formulate an optimization problem with the objective of minimizing the expected execution time for each iteration in the learning process. We develop an efficient algorithm to mathematically solve the problem by outputting the optimum strategy. Extensive simulation results demonstrate the superiority of our schemes compared with conventional solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge