SASSL: Enhancing Self-Supervised Learning via Neural Style Transfer

Self-supervised learning relies heavily on data augmentation to extract meaningful representations from unlabeled images. While existing state-of-the-art augmentation pipelines incorporate a wide range of primitive transformations, these often disregard natural image structure. Thus, augmented samples can exhibit degraded semantic information and low stylistic diversity, affecting downstream performance of self-supervised representations. To overcome this, we propose SASSL: Style Augmentations for Self Supervised Learning, a novel augmentation technique based on Neural Style Transfer. The method decouples semantic and stylistic attributes in images and applies transformations exclusively to the style while preserving content, generating diverse augmented samples that better retain their semantic properties. Experimental results show our technique achieves a top-1 classification performance improvement of more than 2% on ImageNet compared to the well-established MoCo v2. We also measure transfer learning performance across five diverse datasets, observing significant improvements of up to 3.75%. Our experiments indicate that decoupling style from content information and transferring style across datasets to diversify augmentations can significantly improve downstream performance of self-supervised representations.

PAC$^m$-Bayes: Narrowing the Empirical Risk Gap in the Misspecified Bayesian Regime

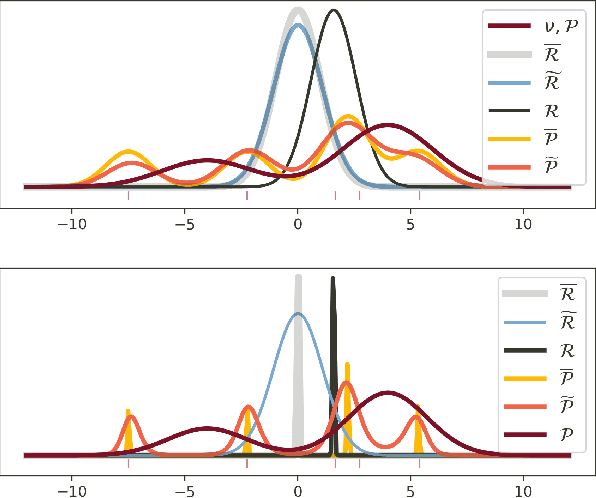
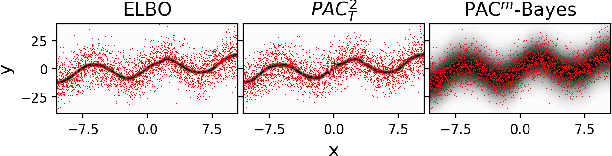
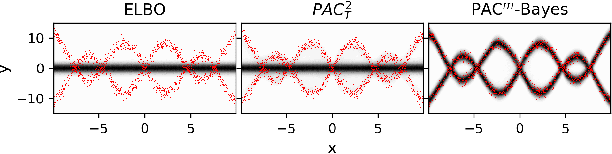
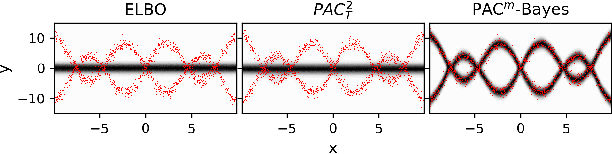
While the decision-theoretic optimality of the Bayesian formalism under correct model specification is well-known (Berger 2013), the Bayesian case becomes less clear under model misspecification (Grunwald 2017; Ramamoorthi 2015; Fushiki 2005). To formally understand the consequences of Bayesian misspecification, this work examines the relationship between posterior predictive risk and its sensitivity to correct model assumptions, i.e., choice of likelihood and prior. We present the multisample PAC$^m$-Bayes risk. This risk is justified by theoretical analysis based on PAC-Bayes as well as empirical study on a number of toy problems. The PAC$^m$-Bayes risk is appealing in that it entails direct minimization of the Monte-Carlo approximated posterior predictive risk yet recovers both the Bayesian formalism as well as the MLE in its limits. Our work is heavily influenced by Masegosa (2019); our contributions are to align training and generalization risks while offering a tighter bound which empirically performs at least as well and sometimes much better.

Density of States Estimation for Out-of-Distribution Detection

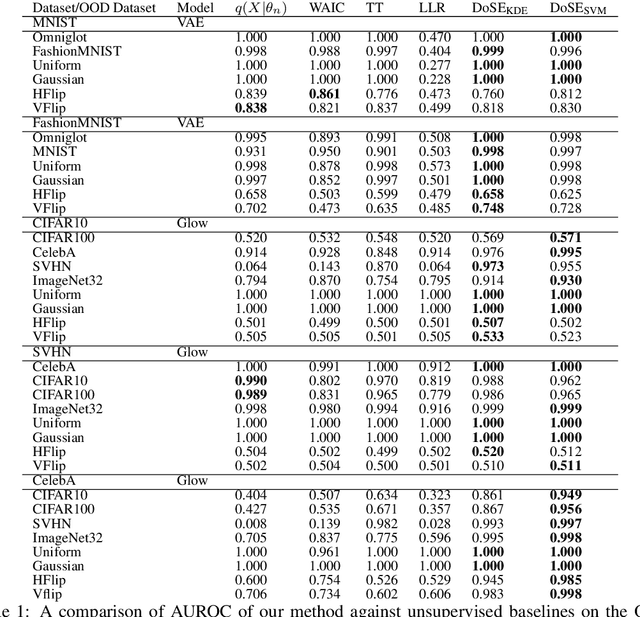
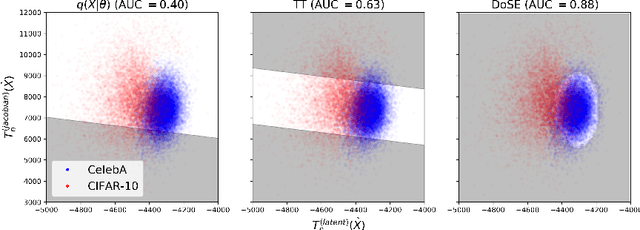
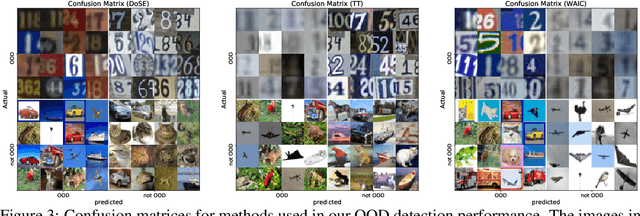
Perhaps surprisingly, recent studies have shown probabilistic model likelihoods have poor specificity for out-of-distribution (OOD) detection and often assign higher likelihoods to OOD data than in-distribution data. To ameliorate this issue we propose DoSE, the density of states estimator. Drawing on the statistical physics notion of ``density of states,'' the DoSE decision rule avoids direct comparison of model probabilities, and instead utilizes the ``probability of the model probability,'' or indeed the frequency of any reasonable statistic. The frequency is calculated using nonparametric density estimators (e.g., KDE and one-class SVM) which measure the typicality of various model statistics given the training data and from which we can flag test points with low typicality as anomalous. Unlike many other methods, DoSE requires neither labeled data nor OOD examples. DoSE is modular and can be trivially applied to any existing, trained model. We demonstrate DoSE's state-of-the-art performance against other unsupervised OOD detectors on previously established ``hard'' benchmarks.

Automatic Differentiation Variational Inference with Mixtures

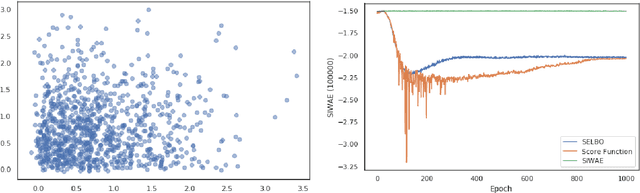
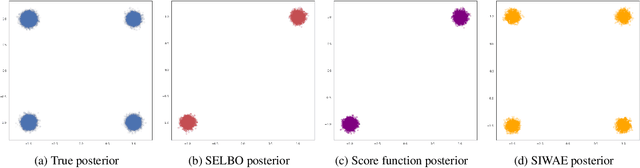
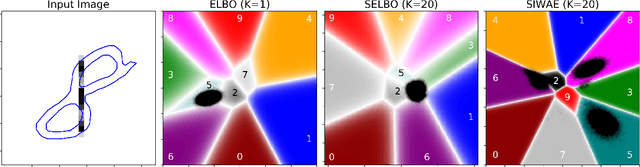
Automatic Differentiation Variational Inference (ADVI) is a useful tool for efficiently learning probabilistic models in machine learning. Generally approximate posteriors learned by ADVI are forced to be unimodal in order to facilitate use of the reparameterization trick. In this paper, we show how stratified sampling may be used to enable mixture distributions as the approximate posterior, and derive a new lower bound on the evidence analogous to the importance weighted autoencoder (IWAE). We show that this "SIWAE" is a tighter bound than both IWAE and the traditional ELBO, both of which are special instances of this bound. We verify empirically that the traditional ELBO objective disfavors the presence of multimodal posterior distributions and may therefore not be able to fully capture structure in the latent space. Our experiments show that using the SIWAE objective allows the encoder to learn more complex distributions which regularly contain multimodality, resulting in higher accuracy and better calibration in the presence of incomplete, limited, or corrupted data.