A Hybrid Brain-Computer Interface Using Motor Imagery and SSVEP Based on Convolutional Neural Network

The key to electroencephalography (EEG)-based brain-computer interface (BCI) lies in neural decoding, and its accuracy can be improved by using hybrid BCI paradigms, that is, fusing multiple paradigms. However, hybrid BCIs usually require separate processing processes for EEG signals in each paradigm, which greatly reduces the efficiency of EEG feature extraction and the generalizability of the model. Here, we propose a two-stream convolutional neural network (TSCNN) based hybrid brain-computer interface. It combines steady-state visual evoked potential (SSVEP) and motor imagery (MI) paradigms. TSCNN automatically learns to extract EEG features in the two paradigms in the training process, and improves the decoding accuracy by 25.4% compared with the MI mode, and 2.6% compared with SSVEP mode in the test data. Moreover, the versatility of TSCNN is verified as it provides considerable performance in both single-mode (70.2% for MI, 93.0% for SSVEP) and hybrid-mode scenarios (95.6% for MI-SSVEP hybrid). Our work will facilitate the real-world applications of EEG-based BCI systems.

Partial Least Square Regression via Three-factor SVD-type Manifold Optimization for EEG Decoding

Partial least square regression (PLSR) is a widely-used statistical model to reveal the linear relationships of latent factors that comes from the independent variables and dependent variables. However, traditional methods to solve PLSR models are usually based on the Euclidean space, and easily getting stuck into a local minimum. To this end, we propose a new method to solve the partial least square regression, named PLSR via optimization on bi-Grassmann manifold (PLSRbiGr). Specifically, we first leverage the three-factor SVD-type decomposition of the cross-covariance matrix defined on the bi-Grassmann manifold, converting the orthogonal constrained optimization problem into an unconstrained optimization problem on bi-Grassmann manifold, and then incorporate the Riemannian preconditioning of matrix scaling to regulate the Riemannian metric in each iteration. PLSRbiGr is validated with a variety of experiments for decoding EEG signals at motor imagery (MI) and steady-state visual evoked potential (SSVEP) task. Experimental results demonstrate that PLSRbiGr outperforms competing algorithms in multiple EEG decoding tasks, which will greatly facilitate small sample data learning.

HyperNTF: A Hypergraph Regularized Nonnegative Tensor Factorization for Dimensionality Reduction

Most methods for dimensionality reduction are based on either tensor representation or local geometry learning. However, the tensor-based methods severely rely on the assumption of global and multilinear structures in high-dimensional data; and the manifold learning methods suffer from the out-of-sample problem. In this paper, bridging the tensor decomposition and manifold learning, we propose a novel method, called Hypergraph Regularized Nonnegative Tensor Factorization (HyperNTF). HyperNTF can preserve nonnegativity in tensor factorization, and uncover the higher-order relationship among the nearest neighborhoods. Clustering analysis with HyperNTF has low computation and storage costs. The experiments on four synthetic data show a desirable property of hypergraph in uncovering the high-order correlation to unfold the curved manifolds. Moreover, the numerical experiments on six real datasets suggest that HyperNTF robustly outperforms state-of-the-art algorithms in clustering analysis.

Riemannian-based Discriminant Analysis for Feature Extraction and Classification

Discriminant analysis, as a widely used approach in machine learning to extract low-dimensional features from the high-dimensional data, applies the Fisher discriminant criterion to find the orthogonal discriminant projection subspace. But most of the Euclidean-based algorithms for discriminant analysis are easily convergent to a spurious local minima and hardly obtain an unique solution. To address such problem, in this study we propose a novel method named Riemannian-based Discriminant Analysis (RDA), which transforms the traditional Euclidean-based methods to the Riemannian manifold space. In RDA, the second-order geometry of trust-region methods is utilized to learn the discriminant bases. To validate the efficiency and effectiveness of RDA, we conduct a variety of experiments on image classification tasks. The numerical results suggest that RDA can extract statistically significant features and robustly outperform state-of-the-art algorithms in classification tasks.

Experimental Analysis of Legendre Decomposition in Machine Learning

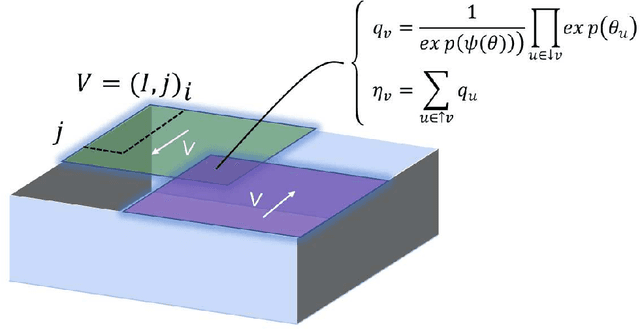
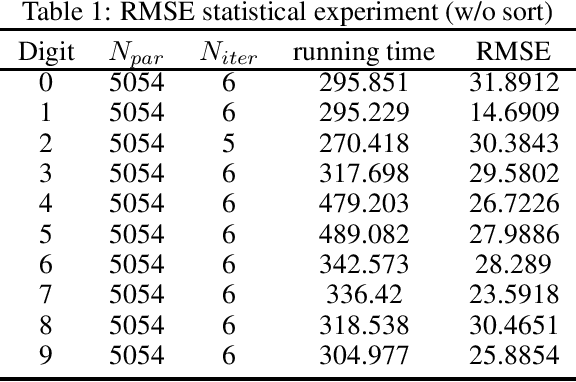
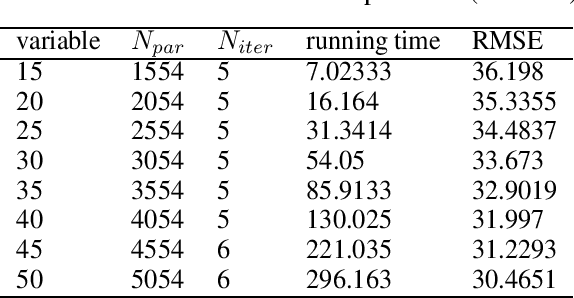
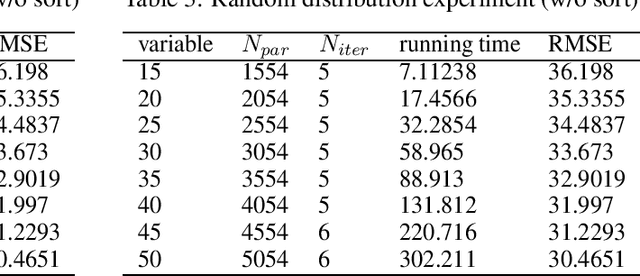
In this technical report, we analyze Legendre decomposition for non-negative tensor in theory and application. In theory, the properties of dual parameters and dually flat manifold in Legendre decomposition are reviewed, and the process of tensor projection and parameter updating is analyzed. In application, a series of verification experiments and clustering experiments with parameters in submanifolds are carried out, hoping to find an effective lower dimensional representation of the input tensor. The experimental results show that the parameters in submanifolds have no ability to be directly represented as low-rank representations. Combined with analysis, we connect Legendre decomposition with neural networks and low-rank representation, and put forward some promising prospects.