Experimental Analysis of Legendre Decomposition in Machine Learning

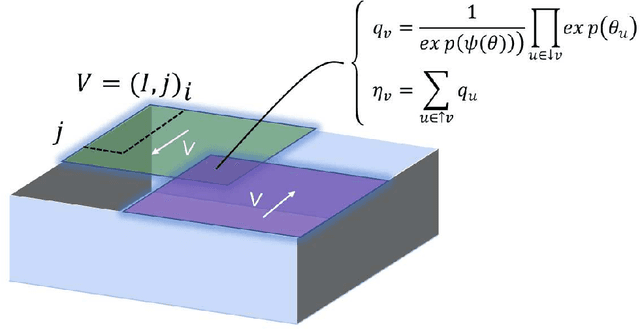
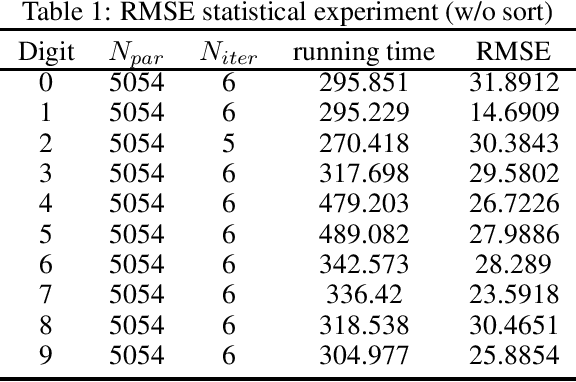
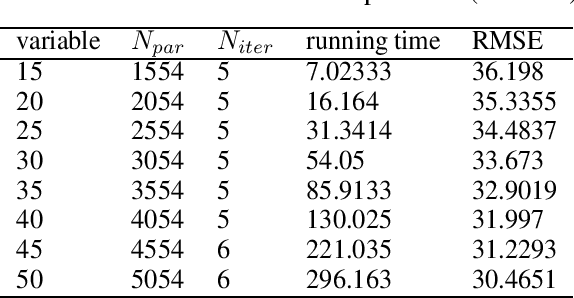
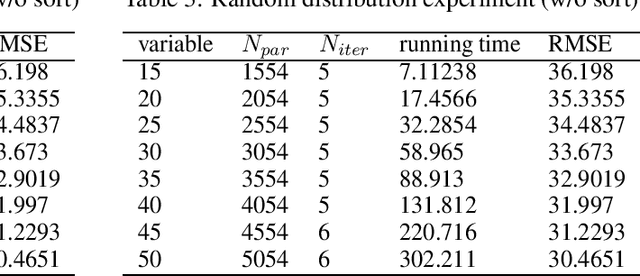
In this technical report, we analyze Legendre decomposition for non-negative tensor in theory and application. In theory, the properties of dual parameters and dually flat manifold in Legendre decomposition are reviewed, and the process of tensor projection and parameter updating is analyzed. In application, a series of verification experiments and clustering experiments with parameters in submanifolds are carried out, hoping to find an effective lower dimensional representation of the input tensor. The experimental results show that the parameters in submanifolds have no ability to be directly represented as low-rank representations. Combined with analysis, we connect Legendre decomposition with neural networks and low-rank representation, and put forward some promising prospects.