PICProp: Physics-Informed Confidence Propagation for Uncertainty Quantification

Standard approaches for uncertainty quantification in deep learning and physics-informed learning have persistent limitations. Indicatively, strong assumptions regarding the data likelihood are required, the performance highly depends on the selection of priors, and the posterior can be sampled only approximately, which leads to poor approximations because of the associated computational cost. This paper introduces and studies confidence interval (CI) estimation for deterministic partial differential equations as a novel problem. That is, to propagate confidence, in the form of CIs, from data locations to the entire domain with probabilistic guarantees. We propose a method, termed Physics-Informed Confidence Propagation (PICProp), based on bi-level optimization to compute a valid CI without making heavy assumptions. We provide a theorem regarding the validity of our method, and computational experiments, where the focus is on physics-informed learning.

MixupE: Understanding and Improving Mixup from Directional Derivative Perspective

Mixup is a popular data augmentation technique for training deep neural networks where additional samples are generated by linearly interpolating pairs of inputs and their labels. This technique is known to improve the generalization performance in many learning paradigms and applications. In this work, we first analyze Mixup and show that it implicitly regularizes infinitely many directional derivatives of all orders. We then propose a new method to improve Mixup based on the novel insight. To demonstrate the effectiveness of the proposed method, we conduct experiments across various domains such as images, tabular data, speech, and graphs. Our results show that the proposed method improves Mixup across various datasets using a variety of architectures, for instance, exhibiting an improvement over Mixup by 0.8% in ImageNet top-1 accuracy.

Model identification for ARMA time series through convolutional neural networks

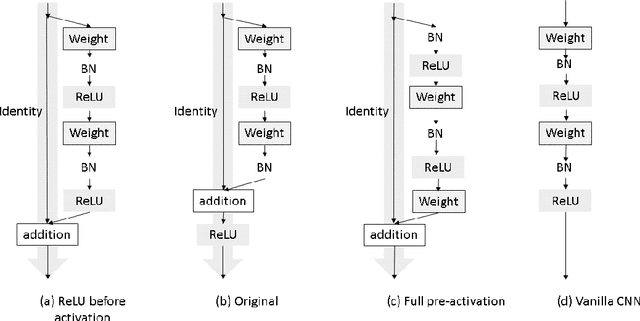
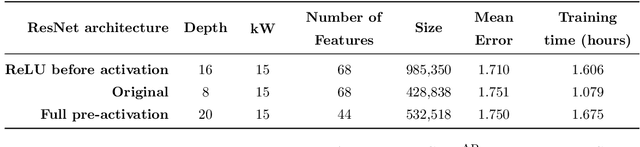
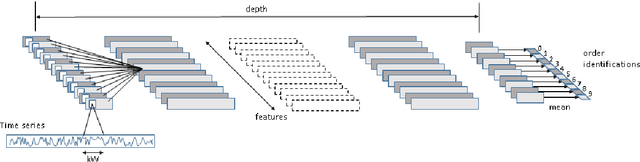
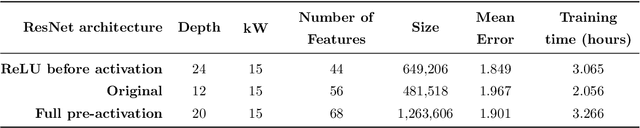
In this paper, we use convolutional neural networks to address the problem of model identification for autoregressive moving average time series models. We compare the performance of several neural network architectures, trained on simulated time series, with likelihood based methods, in particular the Akaike and Bayesian information criteria. We find that our neural networks can significantly outperform these likelihood based methods in terms of accuracy and, by orders of magnitude, in terms of speed.