Vincent Thomas
LORIA/INRIA
Partially Observable Monte-Carlo Graph Search
Jul 28, 2025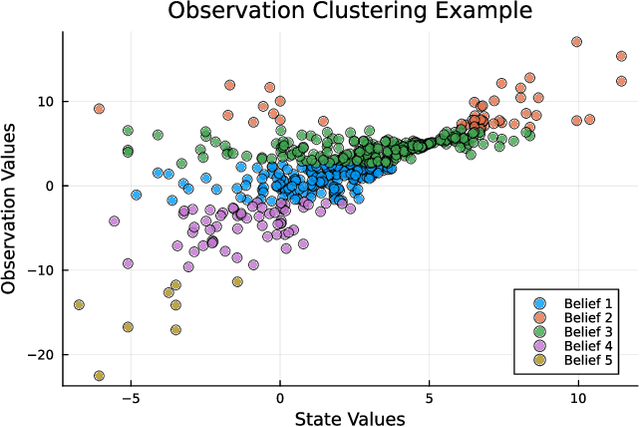

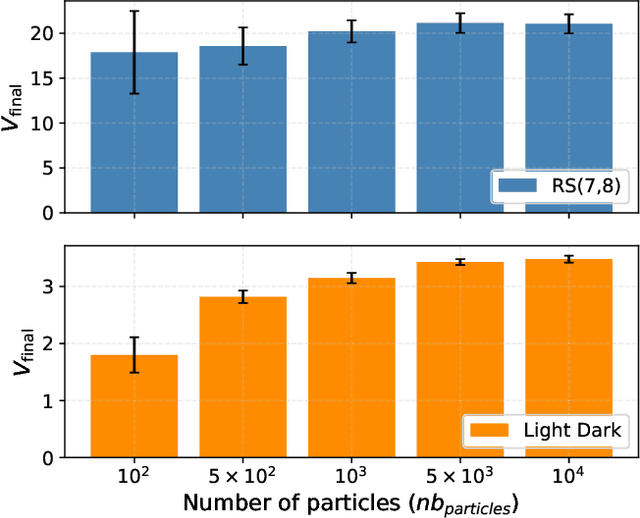

Abstract:Currently, large partially observable Markov decision processes (POMDPs) are often solved by sampling-based online methods which interleave planning and execution phases. However, a pre-computed offline policy is more desirable in POMDP applications with time or energy constraints. But previous offline algorithms are not able to scale up to large POMDPs. In this article, we propose a new sampling-based algorithm, the partially observable Monte-Carlo graph search (POMCGS) to solve large POMDPs offline. Different from many online POMDP methods, which progressively develop a tree while performing (Monte-Carlo) simulations, POMCGS folds this search tree on the fly to construct a policy graph, so that computations can be drastically reduced, and users can analyze and validate the policy prior to embedding and executing it. Moreover, POMCGS, together with action progressive widening and observation clustering methods provided in this article, is able to address certain continuous POMDPs. Through experiments, we demonstrate that POMCGS can generate policies on the most challenging POMDPs, which cannot be computed by previous offline algorithms, and these policies' values are competitive compared with the state-of-the-art online POMDP algorithms.
How to Exhibit More Predictable Behaviors
Apr 17, 2024



Abstract:This paper looks at predictability problems, i.e., wherein an agent must choose its strategy in order to optimize the predictions that an external observer could make. We address these problems while taking into account uncertainties on the environment dynamics and on the observed agent's policy. To that end, we assume that the observer 1. seeks to predict the agent's future action or state at each time step, and 2. models the agent using a stochastic policy computed from a known underlying problem, and we leverage on the framework of observer-aware Markov decision processes (OAMDPs). We propose action and state predictability performance criteria through reward functions built on the observer's belief about the agent policy; show that these induced predictable OAMDPs can be represented by goal-oriented or discounted MDPs; and analyze the properties of the proposed reward functions both theoretically and empirically on two types of grid-world problems.
Monte-Carlo Search for an Equilibrium in Dec-POMDPs
May 19, 2023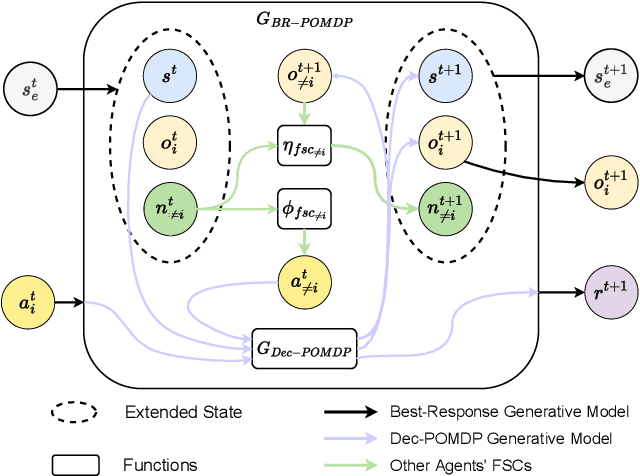
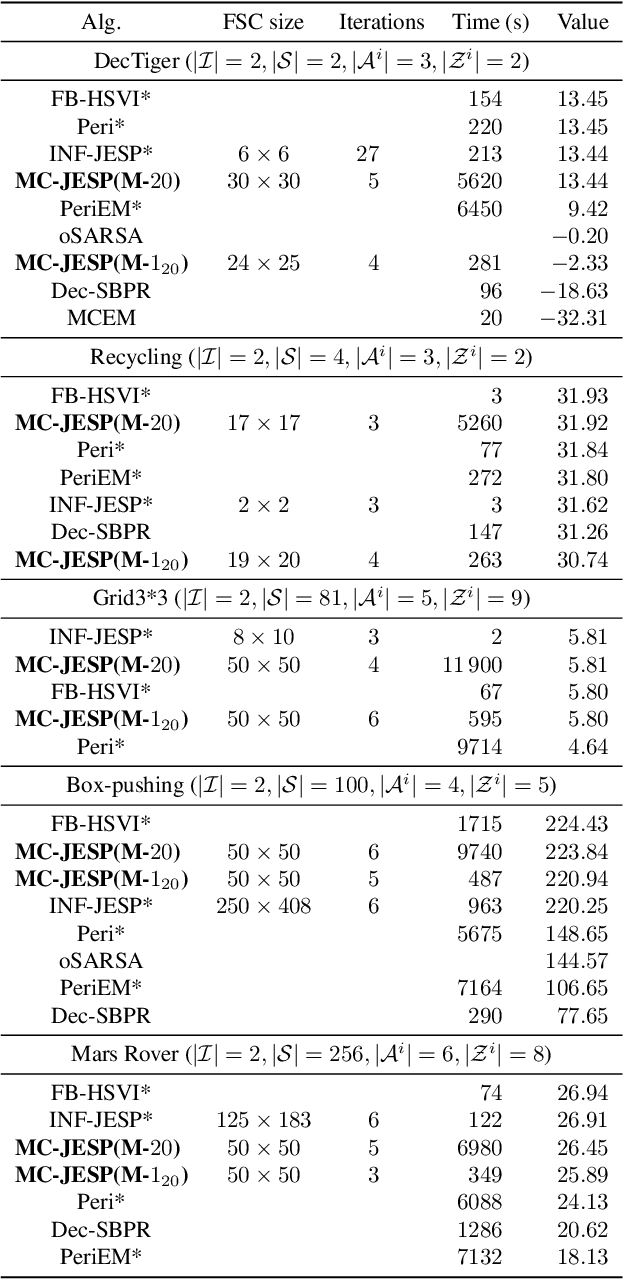
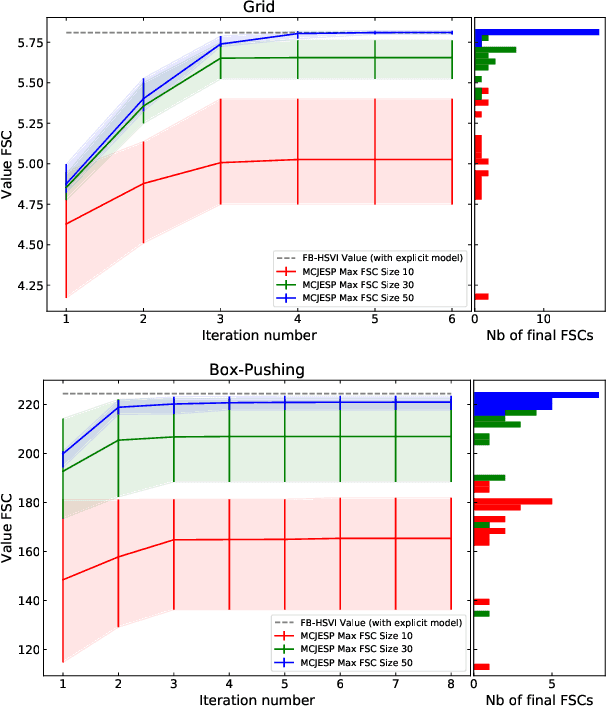
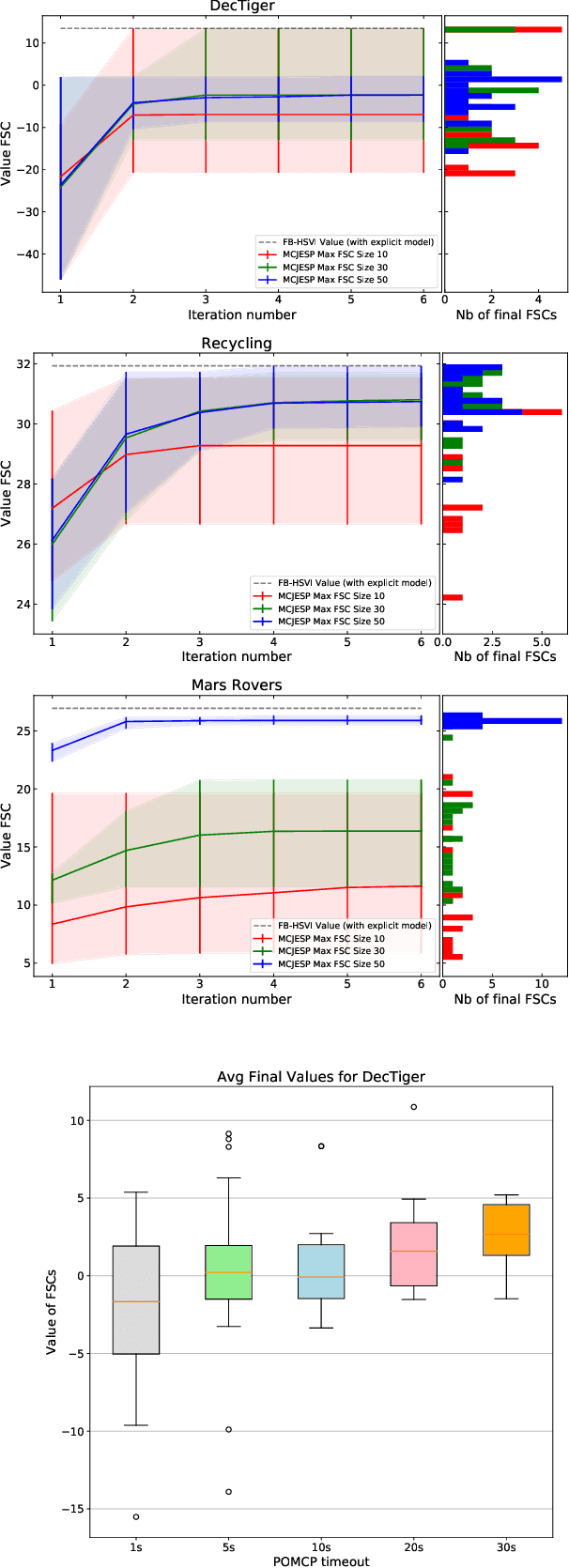
Abstract:Decentralized partially observable Markov decision processes (Dec-POMDPs) formalize the problem of designing individual controllers for a group of collaborative agents under stochastic dynamics and partial observability. Seeking a global optimum is difficult (NEXP complete), but seeking a Nash equilibrium -- each agent policy being a best response to the other agents -- is more accessible, and allowed addressing infinite-horizon problems with solutions in the form of finite state controllers. In this paper, we show that this approach can be adapted to cases where only a generative model (a simulator) of the Dec-POMDP is available. This requires relying on a simulation-based POMDP solver to construct an agent's FSC node by node. A related process is used to heuristically derive initial FSCs. Experiment with benchmarks shows that MC-JESP is competitive with exisiting Dec-POMDP solvers, even better than many offline methods using explicit models.
Robust Robot Planning for Human-Robot Collaboration
Feb 27, 2023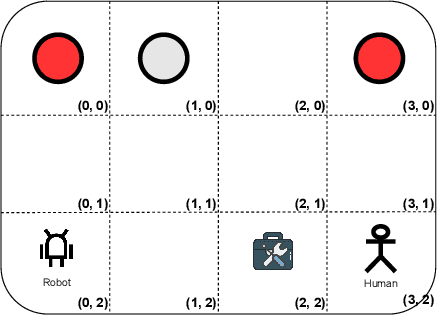
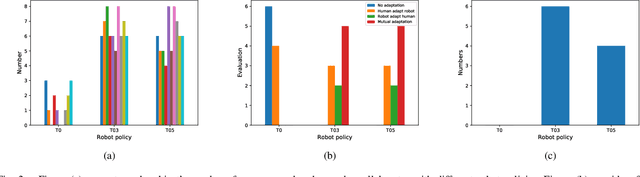
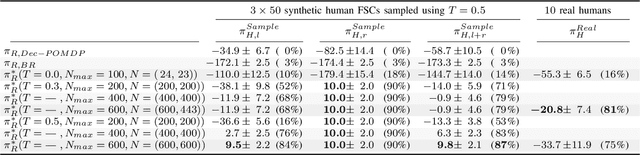
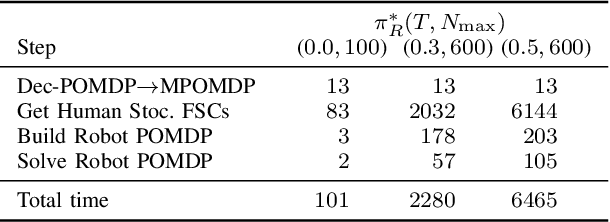
Abstract:In human-robot collaboration, the objectives of the human are often unknown to the robot. Moreover, even assuming a known objective, the human behavior is also uncertain. In order to plan a robust robot behavior, a key preliminary question is then: How to derive realistic human behaviors given a known objective? A major issue is that such a human behavior should itself account for the robot behavior, otherwise collaboration cannot happen. In this paper, we rely on Markov decision models, representing the uncertainty over the human objective as a probability distribution over a finite set of objective functions (inducing a distribution over human behaviors). Based on this, we propose two contributions: 1) an approach to automatically generate an uncertain human behavior (a policy) for each given objective function while accounting for possible robot behaviors; and 2) a robot planning algorithm that is robust to the above-mentioned uncertainties and relies on solving a partially observable Markov decision process (POMDP) obtained by reasoning on a distribution over human behaviors. A co-working scenario allows conducting experiments and presenting qualitative and quantitative results to evaluate our approach.
Solving infinite-horizon Dec-POMDPs using Finite State Controllers within JESP
Sep 17, 2021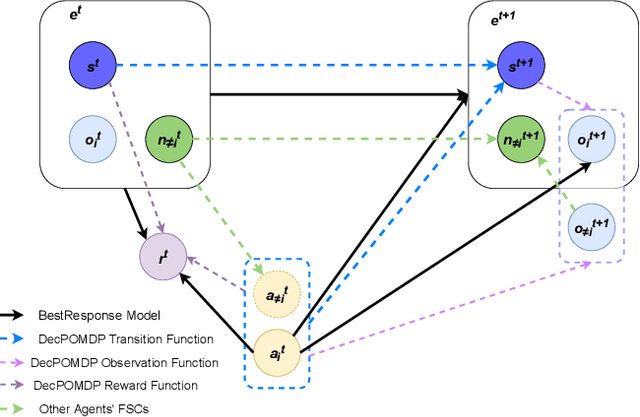
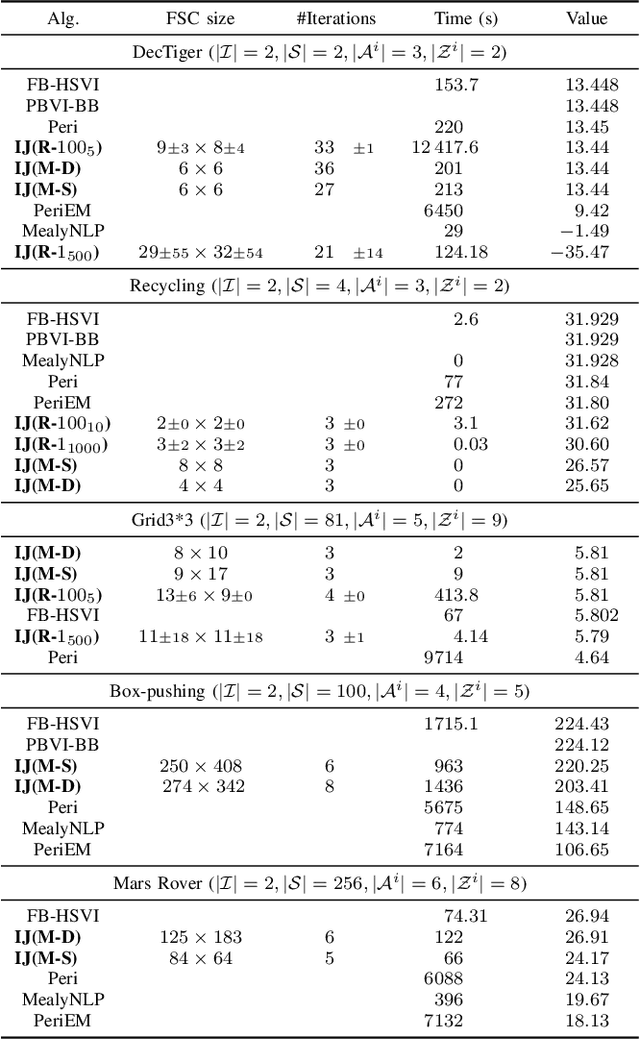
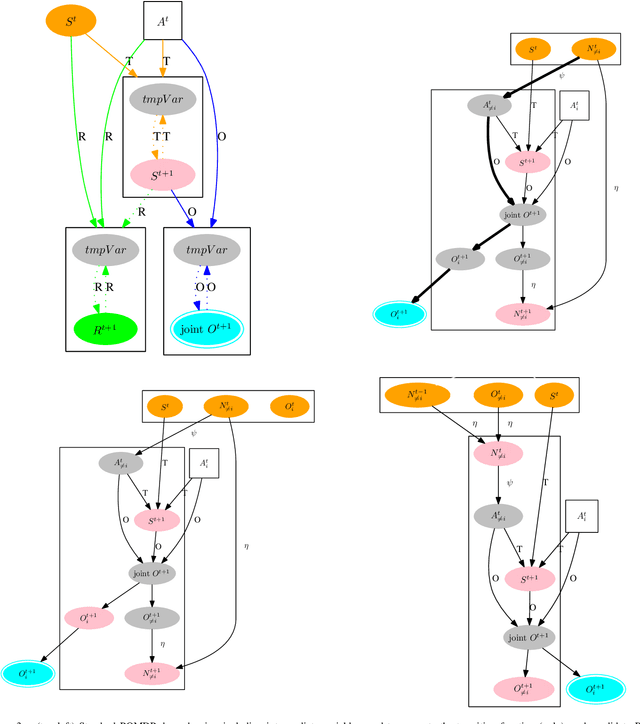
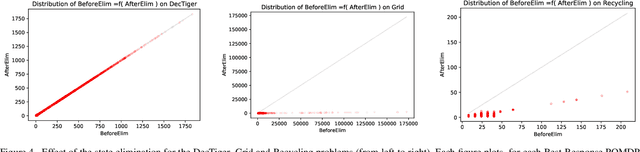
Abstract:This paper looks at solving collaborative planning problems formalized as Decentralized POMDPs (Dec-POMDPs) by searching for Nash equilibria, i.e., situations where each agent's policy is a best response to the other agents' (fixed) policies. While the Joint Equilibrium-based Search for Policies (JESP) algorithm does this in the finite-horizon setting relying on policy trees, we propose here to adapt it to infinite-horizon Dec-POMDPs by using finite state controller (FSC) policy representations. In this article, we (1) explain how to turn a Dec-POMDP with $N-1$ fixed FSCs into an infinite-horizon POMDP whose solution is an $N^\text{th}$ agent best response; (2) propose a JESP variant, called \infJESP, using this to solve infinite-horizon Dec-POMDPs; (3) introduce heuristic initializations for JESP aiming at leading to good solutions; and (4) conduct experiments on state-of-the-art benchmark problems to evaluate our approach.
Monte Carlo Information-Oriented Planning
Mar 21, 2021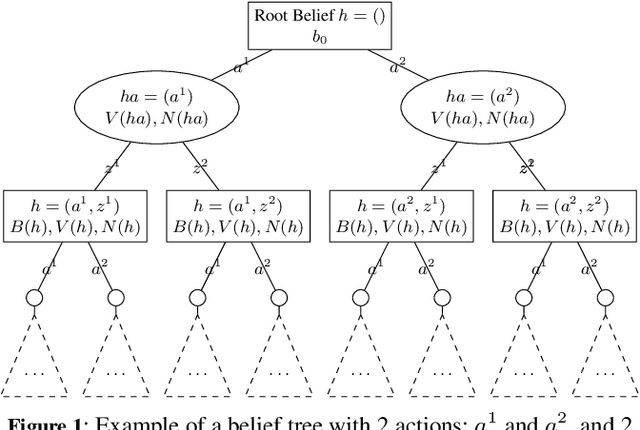
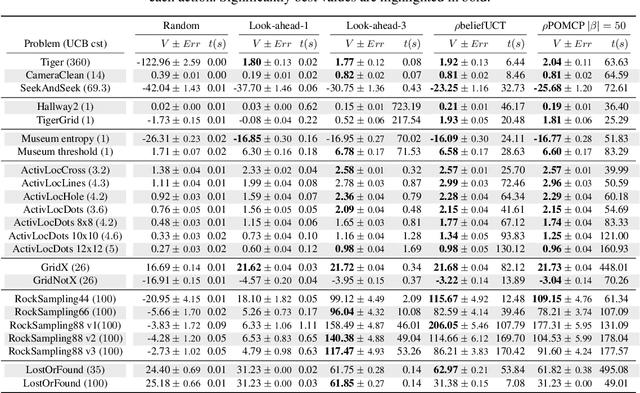
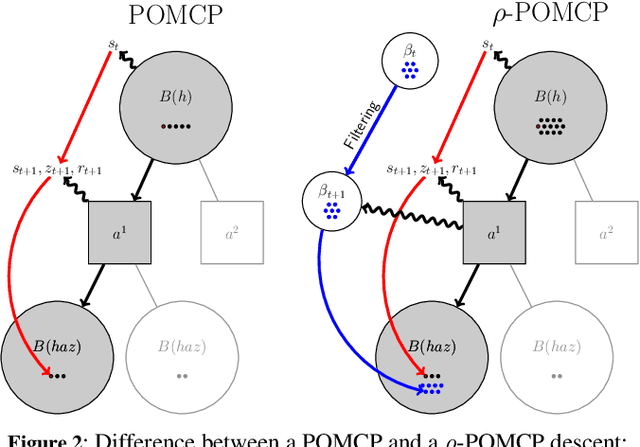
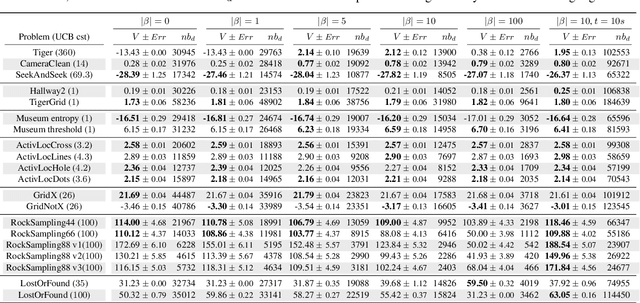
Abstract:In this article, we discuss how to solve information-gathering problems expressed as rho-POMDPs, an extension of Partially Observable Markov Decision Processes (POMDPs) whose reward rho depends on the belief state. Point-based approaches used for solving POMDPs have been extended to solving rho-POMDPs as belief MDPs when its reward rho is convex in B or when it is Lipschitz-continuous. In the present paper, we build on the POMCP algorithm to propose a Monte Carlo Tree Search for rho-POMDPs, aiming for an efficient on-line planner which can be used for any rho function. Adaptations are required due to the belief-dependent rewards to (i) propagate more than one state at a time, and (ii) prevent biases in value estimates. An asymptotic convergence proof to epsilon-optimal values is given when rho is continuous. Experiments are conducted to analyze the algorithms at hand and show that they outperform myopic approaches.
On Bellman's Optimality Principle for zs-POSGs
Jun 29, 2020Abstract:Many non-trivial sequential decision-making problems are efficiently solved by relying on Bellman's optimality principle, i.e., exploiting the fact that sub-problems are nested recursively within the original problem. Here we show how it can apply to (infinite horizon) 2-player zero-sum partially observable stochastic games (zs-POSGs) by (i) taking a central planner's viewpoint, which can only reason on a sufficient statistic called occupancy state, and (ii) turning such problems into zero-sum occupancy Markov games (zs-OMGs). Then, exploiting the Lipschitz-continuity of the value function in occupancy space, one can derive a version of the HSVI algorithm (Heuristic Search Value Iteration) that provably finds an $\epsilon$-Nash equilibrium in finite time.
Near-Optimal BRL using Optimistic Local Transitions
Jun 18, 2012
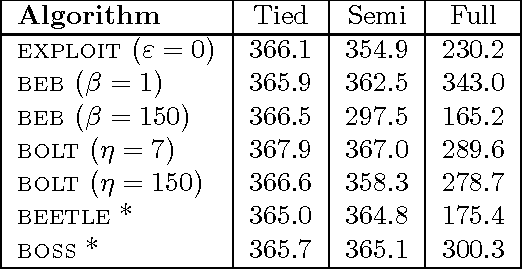
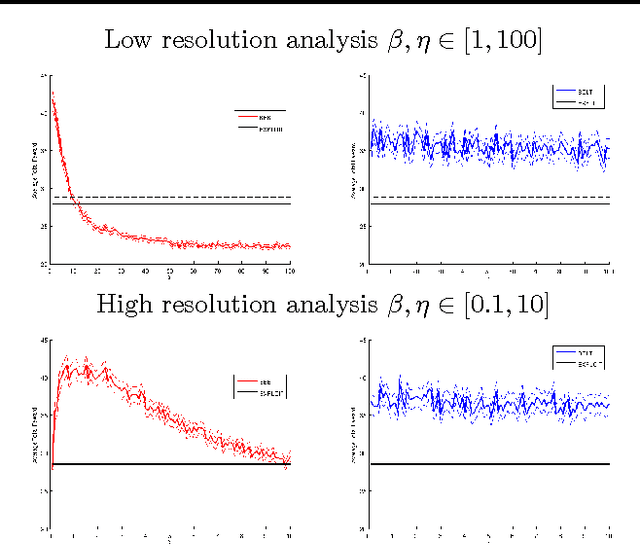

Abstract:Model-based Bayesian Reinforcement Learning (BRL) allows a found formalization of the problem of acting optimally while facing an unknown environment, i.e., avoiding the exploration-exploitation dilemma. However, algorithms explicitly addressing BRL suffer from such a combinatorial explosion that a large body of work relies on heuristic algorithms. This paper introduces BOLT, a simple and (almost) deterministic heuristic algorithm for BRL which is optimistic about the transition function. We analyze BOLT's sample complexity, and show that under certain parameters, the algorithm is near-optimal in the Bayesian sense with high probability. Then, experimental results highlight the key differences of this method compared to previous work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge