Multiresolution and Hierarchical Analysis of Astronomical Spectroscopic Cubes using 3D Discrete Wavelet Transform

The intrinsically hierarchical and blended structure of interstellar molecular clouds, plus the always increasing resolution of astronomical instruments, demand advanced and automated pattern recognition techniques for identifying and connecting source components in spectroscopic cubes. We extend the work done in multiresolution analysis using Wavelets for astronomical 2D images to 3D spectroscopic cubes, combining the results with the Dendrograms approach to offer a hierarchical representation of connections between sources at different scale levels. We test our approach in real data from the ALMA observatory, exploring different Wavelet families and assessing the main parameter for source identification (i.e., RMS) at each level. Our approach shows that is feasible to perform multiresolution analysis for the spatial and frequency domains simultaneously rather than analyzing each spectral channel independently.

A Greedy Approximation of Bayesian Reinforcement Learning with Probably Optimistic Transition Model

Bayesian Reinforcement Learning (RL) is capable of not only incorporating domain knowledge, but also solving the exploration-exploitation dilemma in a natural way. As Bayesian RL is intractable except for special cases, previous work has proposed several approximation methods. However, these methods are usually too sensitive to parameter values, and finding an acceptable parameter setting is practically impossible in many applications. In this paper, we propose a new algorithm that greedily approximates Bayesian RL to achieve robustness in parameter space. We show that for a desired learning behavior, our proposed algorithm has a polynomial sample complexity that is lower than those of existing algorithms. We also demonstrate that the proposed algorithm naturally outperforms other existing algorithms when the prior distributions are not significantly misleading. On the other hand, the proposed algorithm cannot handle greatly misspecified priors as well as the other algorithms can. This is a natural consequence of the fact that the proposed algorithm is greedier than the other algorithms. Accordingly, we discuss a way to select an appropriate algorithm for different tasks based on the algorithms' greediness. We also introduce a new way of simplifying Bayesian planning, based on which future work would be able to derive new algorithms.

Near-Optimal BRL using Optimistic Local Transitions

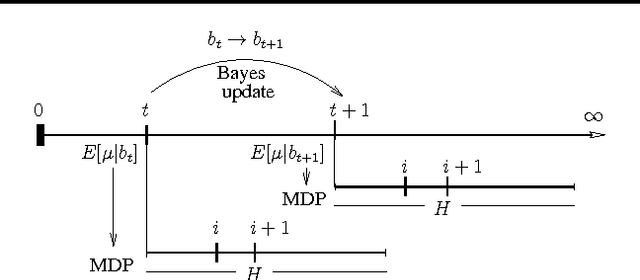
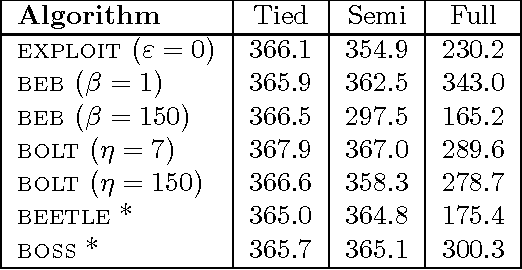
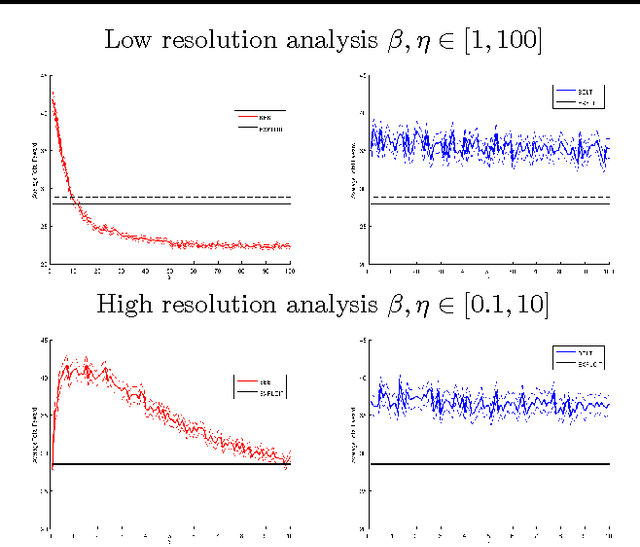
Model-based Bayesian Reinforcement Learning (BRL) allows a found formalization of the problem of acting optimally while facing an unknown environment, i.e., avoiding the exploration-exploitation dilemma. However, algorithms explicitly addressing BRL suffer from such a combinatorial explosion that a large body of work relies on heuristic algorithms. This paper introduces BOLT, a simple and (almost) deterministic heuristic algorithm for BRL which is optimistic about the transition function. We analyze BOLT's sample complexity, and show that under certain parameters, the algorithm is near-optimal in the Bayesian sense with high probability. Then, experimental results highlight the key differences of this method compared to previous work.