Optimally Solving Simultaneous-Move Dec-POMDPs: The Sequential Central Planning Approach

Centralized training for decentralized execution paradigm emerged as the state-of-the-art approach to epsilon-optimally solving decentralized partially observable Markov decision processes. However, scalability remains a significant issue. This paper presents a novel and more scalable alternative, namely sequential-move centralized training for decentralized execution. This paradigm further pushes the applicability of Bellman's principle of optimality, raising three new properties. First, it allows a central planner to reason upon sufficient sequential-move statistics instead of prior simultaneous-move ones. Next, it proves that epsilon-optimal value functions are piecewise linear and convex in sufficient sequential-move statistics. Finally, it drops the complexity of the backup operators from double exponential to polynomial at the expense of longer planning horizons. Besides, it makes it easy to use single-agent methods, e.g., SARSA algorithm enhanced with these findings applies while still preserving convergence guarantees. Experiments on two- as well as many-agent domains from the literature against epsilon-optimal simultaneous-move solvers confirm the superiority of the novel approach. This paradigm opens the door for efficient planning and reinforcement learning methods for multi-agent systems.

Solving Hierarchical Information-Sharing Dec-POMDPs: An Extensive-Form Game Approach

A recent theory shows that a multi-player decentralized partially observable Markov decision process can be transformed into an equivalent single-player game, enabling the application of \citeauthor{bellman}'s principle of optimality to solve the single-player game by breaking it down into single-stage subgames. However, this approach entangles the decision variables of all players at each single-stage subgame, resulting in backups with a double-exponential complexity. This paper demonstrates how to disentangle these decision variables while maintaining optimality under hierarchical information sharing, a prominent management style in our society. To achieve this, we apply the principle of optimality to solve any single-stage subgame by breaking it down further into smaller subgames, enabling us to make single-player decisions at a time. Our approach reveals that extensive-form games always exist with solutions to a single-stage subgame, significantly reducing time complexity. Our experimental results show that the algorithms leveraging these findings can scale up to much larger multi-player games without compromising optimality.

HSVI can solve zero-sum Partially Observable Stochastic Games

State-of-the-art methods for solving 2-player zero-sum imperfect information games rely on linear programming or regret minimization, though not on dynamic programming (DP) or heuristic search (HS), while the latter are often at the core of state-of-the-art solvers for other sequential decision-making problems. In partially observable or collaborative settings (e.g., POMDPs and Dec- POMDPs), DP and HS require introducing an appropriate statistic that induces a fully observable problem as well as bounding (convex) approximators of the optimal value function. This approach has succeeded in some subclasses of 2-player zero-sum partially observable stochastic games (zs- POSGs) as well, but how to apply it in the general case still remains an open question. We answer it by (i) rigorously defining an equivalent game to work with, (ii) proving mathematical properties of the optimal value function that allow deriving bounds that come with solution strategies, (iii) proposing for the first time an HSVI-like solver that provably converges to an $\epsilon$-optimal solution in finite time, and (iv) empirically analyzing it. This opens the door to a novel family of promising approaches complementing those relying on linear programming or iterative methods.

HSVI fo zs-POSGs using Concavity, Convexity and Lipschitz Properties

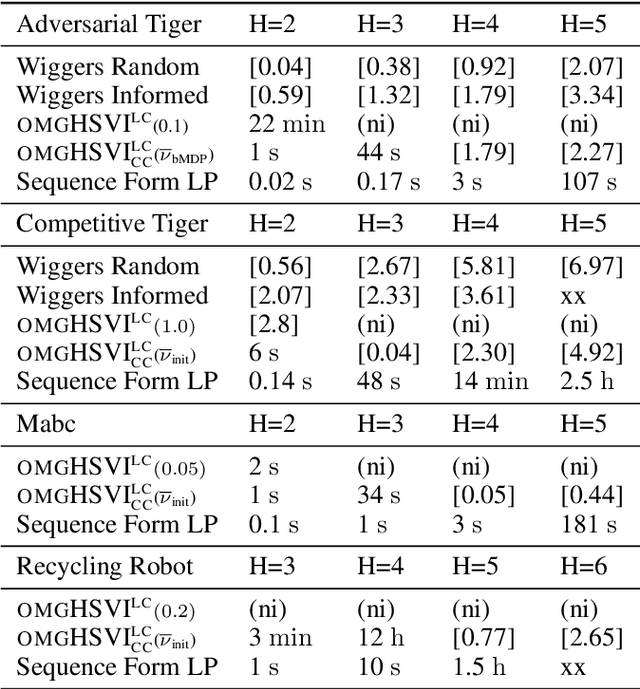
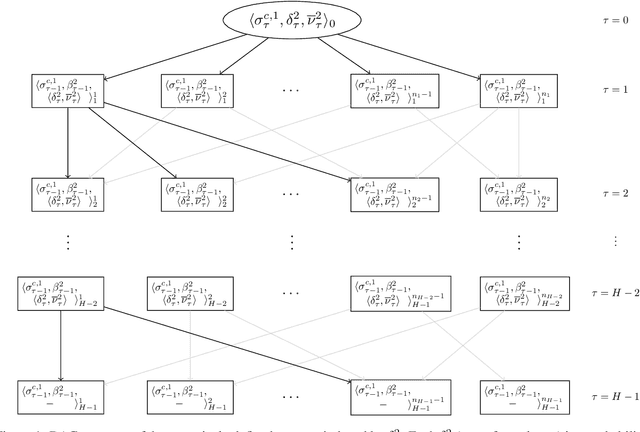
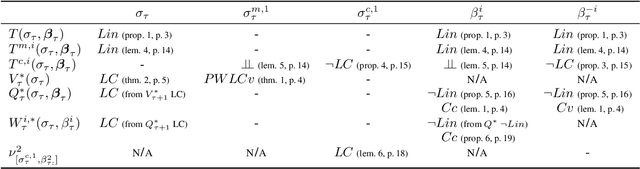
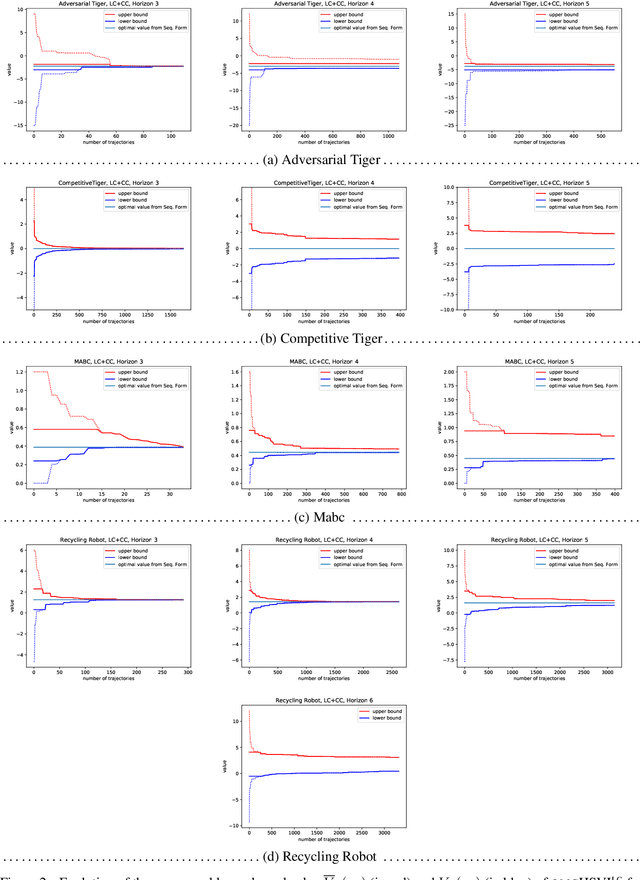
Dynamic programming and heuristic search are at the core of state-of-the-art solvers for sequential decision-making problems. In partially observable or collaborative settings (\eg, POMDPs and Dec-POMDPs), this requires introducing an appropriate statistic that induces a fully observable problem as well as bounding (convex) approximators of the optimal value function. This approach has succeeded in some subclasses of 2-player zero-sum partially observable stochastic games (zs-POSGs) as well, but failed in the general case despite known concavity and convexity properties, which only led to heuristic algorithms with poor convergence guarantees. We overcome this issue, leveraging on these properties to derive bounding approximators and efficient update and selection operators, before deriving a prototypical solver inspired by HSVI that provably converges to an $\epsilon$-optimal solution in finite time, and which we empirically evaluate. This opens the door to a novel family of promising approaches complementing those relying on linear programming or iterative methods.

On Bellman's Optimality Principle for zs-POSGs

Many non-trivial sequential decision-making problems are efficiently solved by relying on Bellman's optimality principle, i.e., exploiting the fact that sub-problems are nested recursively within the original problem. Here we show how it can apply to (infinite horizon) 2-player zero-sum partially observable stochastic games (zs-POSGs) by (i) taking a central planner's viewpoint, which can only reason on a sufficient statistic called occupancy state, and (ii) turning such problems into zero-sum occupancy Markov games (zs-OMGs). Then, exploiting the Lipschitz-continuity of the value function in occupancy space, one can derive a version of the HSVI algorithm (Heuristic Search Value Iteration) that provably finds an $\epsilon$-Nash equilibrium in finite time.