Optimally Solving Simultaneous-Move Dec-POMDPs: The Sequential Central Planning Approach

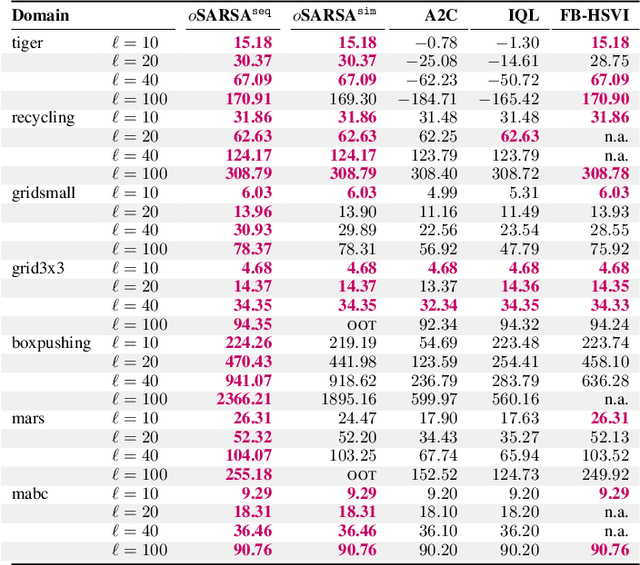
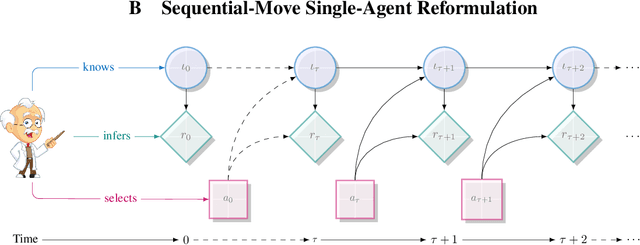
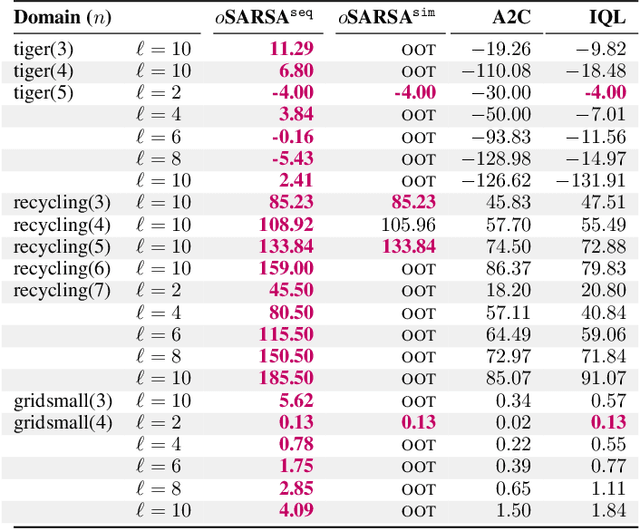
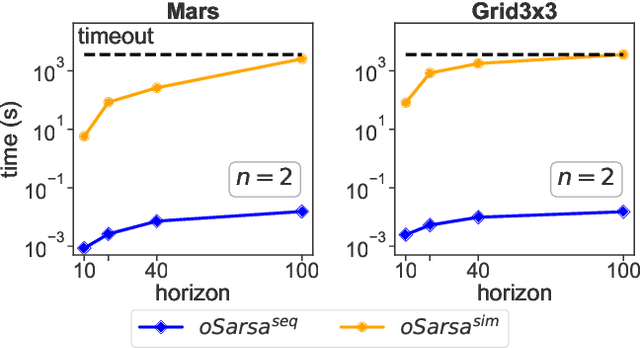
Centralized training for decentralized execution paradigm emerged as the state-of-the-art approach to epsilon-optimally solving decentralized partially observable Markov decision processes. However, scalability remains a significant issue. This paper presents a novel and more scalable alternative, namely sequential-move centralized training for decentralized execution. This paradigm further pushes the applicability of Bellman's principle of optimality, raising three new properties. First, it allows a central planner to reason upon sufficient sequential-move statistics instead of prior simultaneous-move ones. Next, it proves that epsilon-optimal value functions are piecewise linear and convex in sufficient sequential-move statistics. Finally, it drops the complexity of the backup operators from double exponential to polynomial at the expense of longer planning horizons. Besides, it makes it easy to use single-agent methods, e.g., SARSA algorithm enhanced with these findings applies while still preserving convergence guarantees. Experiments on two- as well as many-agent domains from the literature against epsilon-optimal simultaneous-move solvers confirm the superiority of the novel approach. This paradigm opens the door for efficient planning and reinforcement learning methods for multi-agent systems.

Solving Hierarchical Information-Sharing Dec-POMDPs: An Extensive-Form Game Approach

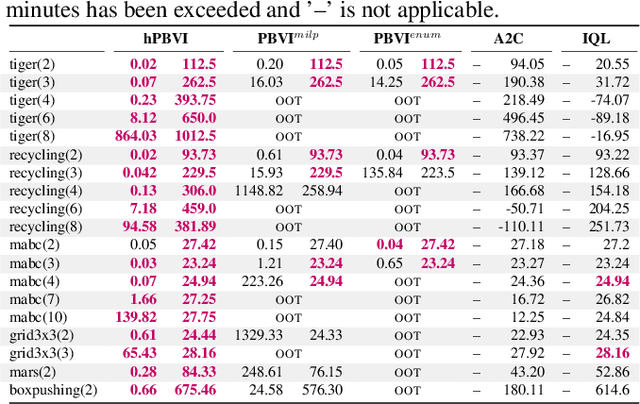
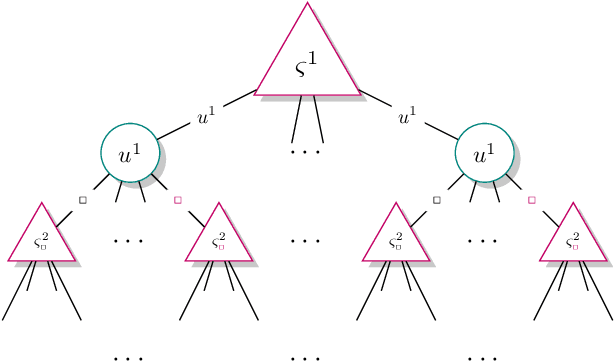
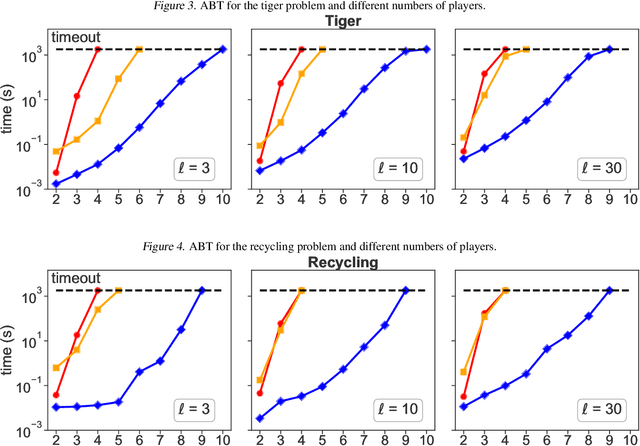
A recent theory shows that a multi-player decentralized partially observable Markov decision process can be transformed into an equivalent single-player game, enabling the application of \citeauthor{bellman}'s principle of optimality to solve the single-player game by breaking it down into single-stage subgames. However, this approach entangles the decision variables of all players at each single-stage subgame, resulting in backups with a double-exponential complexity. This paper demonstrates how to disentangle these decision variables while maintaining optimality under hierarchical information sharing, a prominent management style in our society. To achieve this, we apply the principle of optimality to solve any single-stage subgame by breaking it down further into smaller subgames, enabling us to make single-player decisions at a time. Our approach reveals that extensive-form games always exist with solutions to a single-stage subgame, significantly reducing time complexity. Our experimental results show that the algorithms leveraging these findings can scale up to much larger multi-player games without compromising optimality.