Solving Hierarchical Information-Sharing Dec-POMDPs: An Extensive-Form Game Approach
Paper and Code
Feb 09, 2024
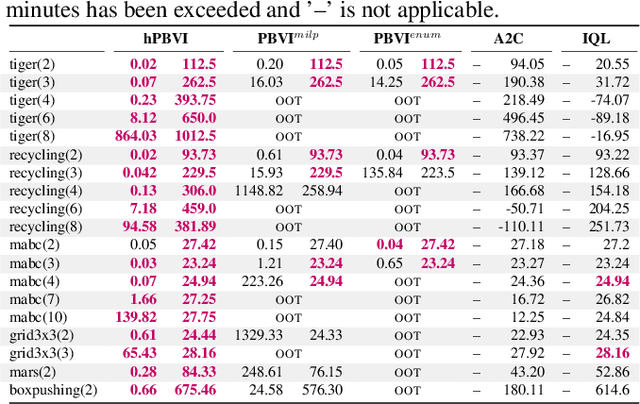
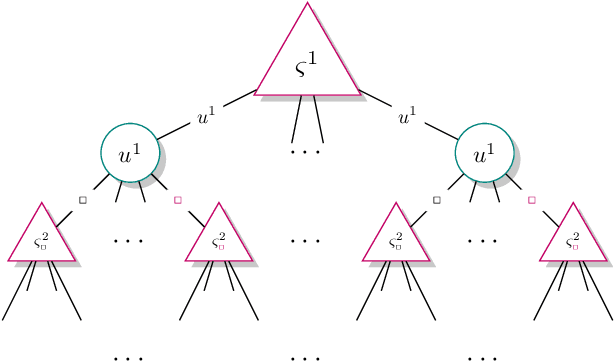
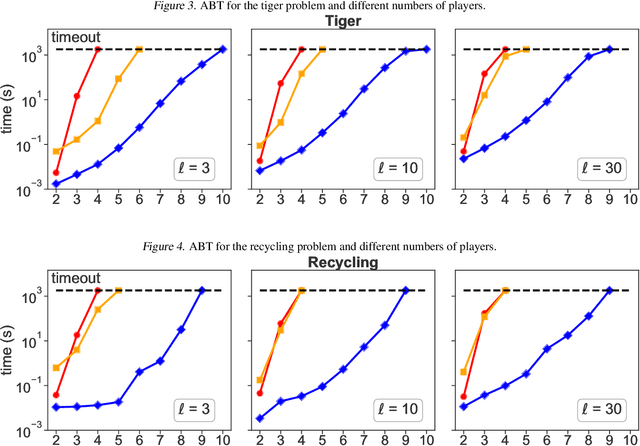
A recent theory shows that a multi-player decentralized partially observable Markov decision process can be transformed into an equivalent single-player game, enabling the application of \citeauthor{bellman}'s principle of optimality to solve the single-player game by breaking it down into single-stage subgames. However, this approach entangles the decision variables of all players at each single-stage subgame, resulting in backups with a double-exponential complexity. This paper demonstrates how to disentangle these decision variables while maintaining optimality under hierarchical information sharing, a prominent management style in our society. To achieve this, we apply the principle of optimality to solve any single-stage subgame by breaking it down further into smaller subgames, enabling us to make single-player decisions at a time. Our approach reveals that extensive-form games always exist with solutions to a single-stage subgame, significantly reducing time complexity. Our experimental results show that the algorithms leveraging these findings can scale up to much larger multi-player games without compromising optimality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge