HSVI fo zs-POSGs using Concavity, Convexity and Lipschitz Properties

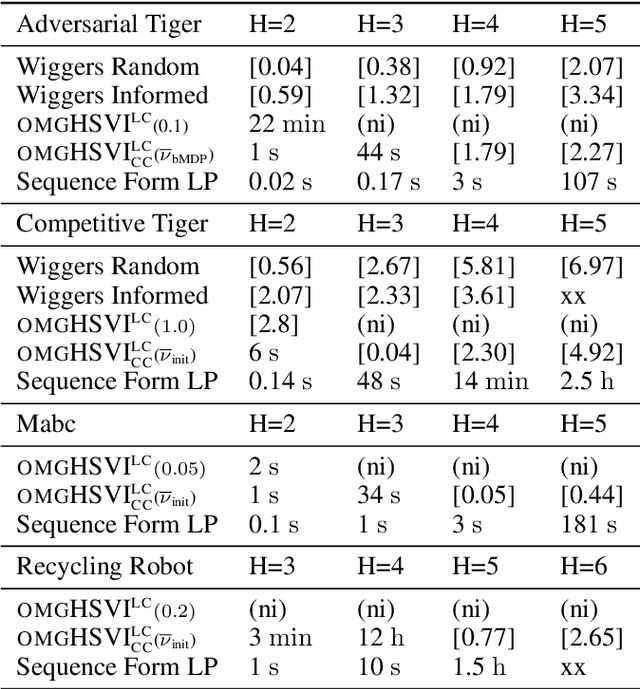
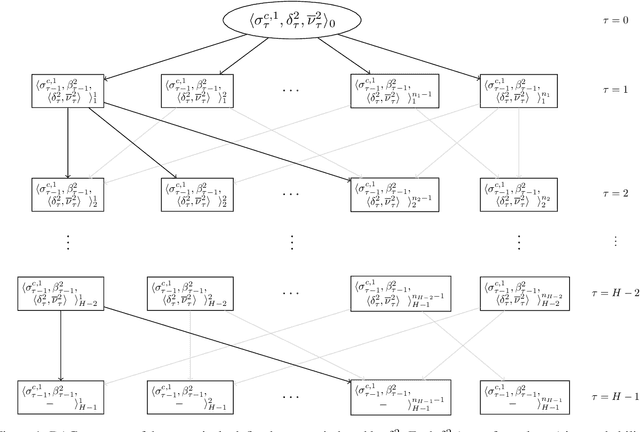
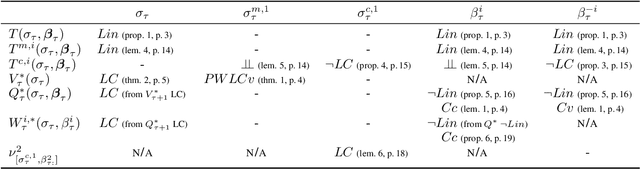
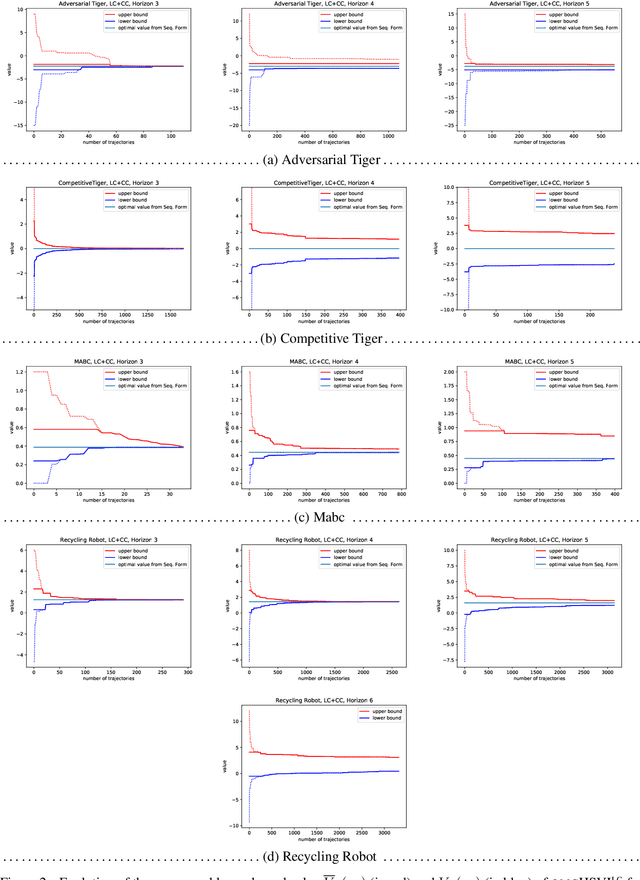
Dynamic programming and heuristic search are at the core of state-of-the-art solvers for sequential decision-making problems. In partially observable or collaborative settings (\eg, POMDPs and Dec-POMDPs), this requires introducing an appropriate statistic that induces a fully observable problem as well as bounding (convex) approximators of the optimal value function. This approach has succeeded in some subclasses of 2-player zero-sum partially observable stochastic games (zs-POSGs) as well, but failed in the general case despite known concavity and convexity properties, which only led to heuristic algorithms with poor convergence guarantees. We overcome this issue, leveraging on these properties to derive bounding approximators and efficient update and selection operators, before deriving a prototypical solver inspired by HSVI that provably converges to an $\epsilon$-optimal solution in finite time, and which we empirically evaluate. This opens the door to a novel family of promising approaches complementing those relying on linear programming or iterative methods.