Gérémy Hutin
Monte Carlo Information-Oriented Planning
Mar 21, 2021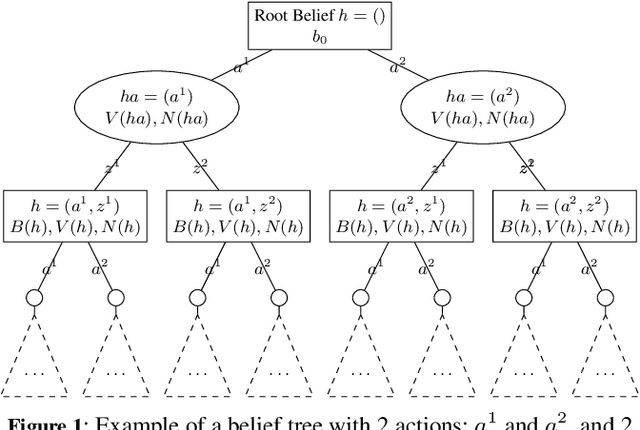
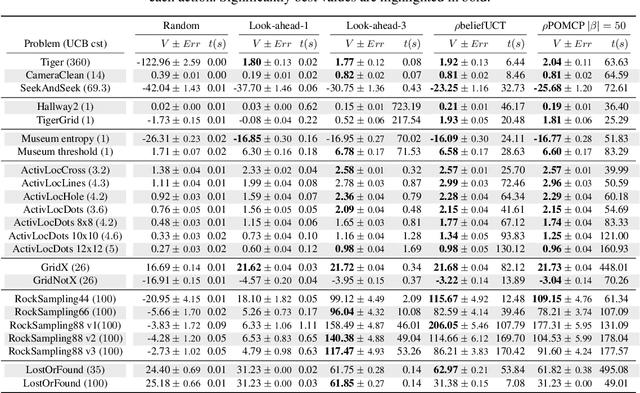
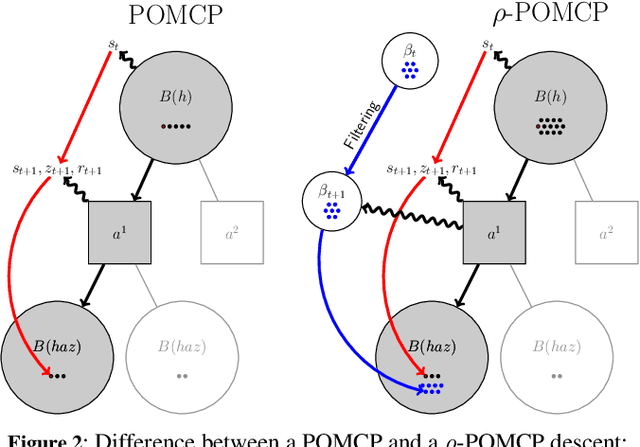
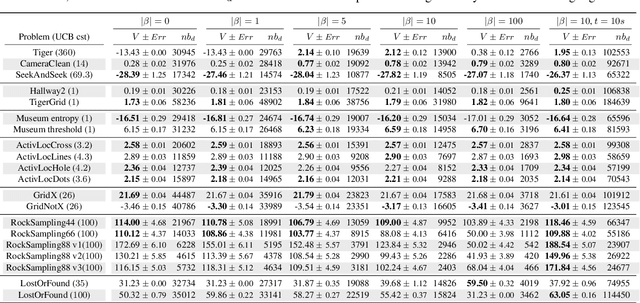
Abstract:In this article, we discuss how to solve information-gathering problems expressed as rho-POMDPs, an extension of Partially Observable Markov Decision Processes (POMDPs) whose reward rho depends on the belief state. Point-based approaches used for solving POMDPs have been extended to solving rho-POMDPs as belief MDPs when its reward rho is convex in B or when it is Lipschitz-continuous. In the present paper, we build on the POMCP algorithm to propose a Monte Carlo Tree Search for rho-POMDPs, aiming for an efficient on-line planner which can be used for any rho function. Adaptations are required due to the belief-dependent rewards to (i) propagate more than one state at a time, and (ii) prevent biases in value estimates. An asymptotic convergence proof to epsilon-optimal values is given when rho is continuous. Experiments are conducted to analyze the algorithms at hand and show that they outperform myopic approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge