Constraint Matters: Multi-Modal Representation for Reducing Mixed-Integer Linear programming

Model reduction, which aims to learn a simpler model of the original mixed integer linear programming (MILP), can solve large-scale MILP problems much faster. Most existing model reduction methods are based on variable reduction, which predicts a solution value for a subset of variables. From a dual perspective, constraint reduction that transforms a subset of inequality constraints into equalities can also reduce the complexity of MILP, but has been largely ignored. Therefore, this paper proposes a novel constraint-based model reduction approach for the MILP. Constraint-based MILP reduction has two challenges: 1) which inequality constraints are critical such that reducing them can accelerate MILP solving while preserving feasibility, and 2) how to predict these critical constraints efficiently. To identify critical constraints, we first label these tight-constraints at the optimal solution as potential critical constraints and design a heuristic rule to select a subset of critical tight-constraints. To learn the critical tight-constraints, we propose a multi-modal representation technique that leverages information from both instance-level and abstract-level MILP formulations. The experimental results show that, compared to the state-of-the-art methods, our method improves the quality of the solution by over 50\% and reduces the computation time by 17.47\%.

Fast and Interpretable Mixed-Integer Linear Program Solving by Learning Model Reduction

By exploiting the correlation between the structure and the solution of Mixed-Integer Linear Programming (MILP), Machine Learning (ML) has become a promising method for solving large-scale MILP problems. Existing ML-based MILP solvers mainly focus on end-to-end solution learning, which suffers from the scalability issue due to the high dimensionality of the solution space. Instead of directly learning the optimal solution, this paper aims to learn a reduced and equivalent model of the original MILP as an intermediate step. The reduced model often corresponds to interpretable operations and is much simpler, enabling us to solve large-scale MILP problems much faster than existing commercial solvers. However, current approaches rely only on the optimal reduced model, overlooking the significant preference information of all reduced models. To address this issue, this paper proposes a preference-based model reduction learning method, which considers the relative performance (i.e., objective cost and constraint feasibility) of all reduced models on each MILP instance as preferences. We also introduce an attention mechanism to capture and represent preference information, which helps improve the performance of model reduction learning tasks. Moreover, we propose a SetCover based pruning method to control the number of reduced models (i.e., labels), thereby simplifying the learning process. Evaluation on real-world MILP problems shows that 1) compared to the state-of-the-art model reduction ML methods, our method obtains nearly 20% improvement on solution accuracy, and 2) compared to the commercial solver Gurobi, two to four orders of magnitude speedups are achieved.

UAV Path Planning for Object Observation with Quality Constraints: A Dynamic Programming Approach

This paper addresses a UAV path planning task that seeks to observe a set of objects while satisfying the observation quality constraint. A dynamic programming algorithm is proposed that enables the UAV to observe the target objects with shortest path while subjecting to the observation quality constraint. The objects have their own facing direction and restricted observation range. With an observing order, the algorithm achieves (1+$\epsilon$)-approximation ratio in theory and runs in polynomial time. The extensive results show that the algorithm produces near-optimal solutions, the effectiveness of which is also tested and proved in the Airsim simulator, a realistic virtual environment.

Too Much Information Kills Information: A Clustering Perspective

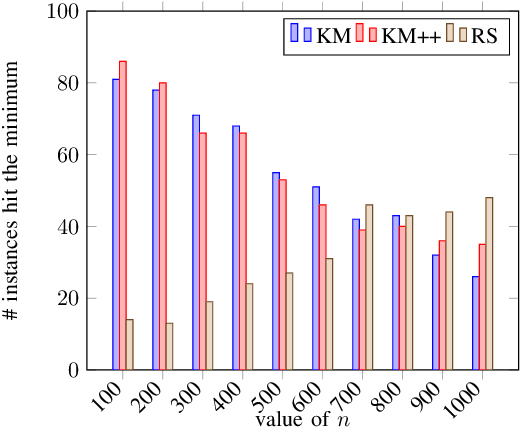
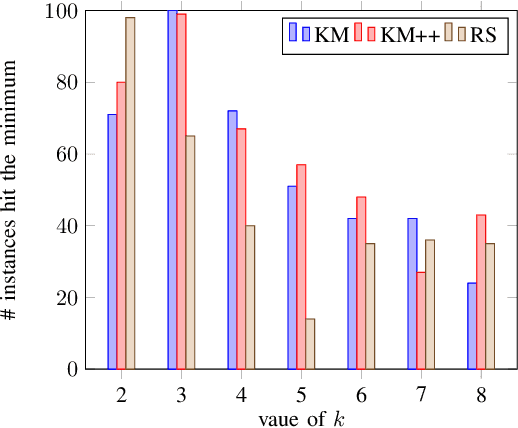
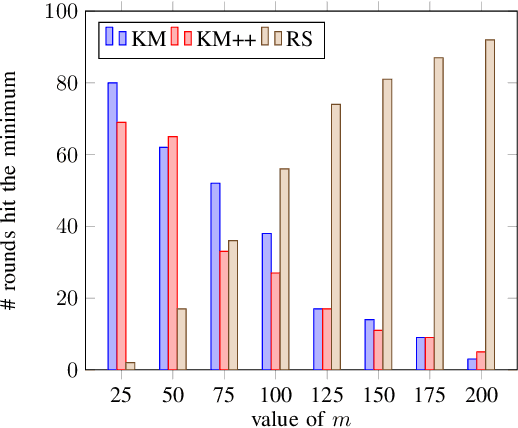
Clustering is one of the most fundamental tools in the artificial intelligence area, particularly in the pattern recognition and learning theory. In this paper, we propose a simple, but novel approach for variance-based k-clustering tasks, included in which is the widely known k-means clustering. The proposed approach picks a sampling subset from the given dataset and makes decisions based on the data information in the subset only. With certain assumptions, the resulting clustering is provably good to estimate the optimum of the variance-based objective with high probability. Extensive experiments on synthetic datasets and real-world datasets show that to obtain competitive results compared with k-means method (Llyod 1982) and k-means++ method (Arthur and Vassilvitskii 2007), we only need 7% information of the dataset. If we have up to 15% information of the dataset, then our algorithm outperforms both the k-means method and k-means++ method in at least 80% of the clustering tasks, in terms of the quality of clustering. Also, an extended algorithm based on the same idea guarantees a balanced k-clustering result.