Set Norm and Equivariant Skip Connections: Putting the Deep in Deep Sets

Permutation invariant neural networks are a promising tool for making predictions from sets. However, we show that existing permutation invariant architectures, Deep Sets and Set Transformer, can suffer from vanishing or exploding gradients when they are deep. Additionally, layer norm, the normalization of choice in Set Transformer, can hurt performance by removing information useful for prediction. To address these issues, we introduce the clean path principle for equivariant residual connections and develop set norm, a normalization tailored for sets. With these, we build Deep Sets++ and Set Transformer++, models that reach high depths with comparable or better performance than their original counterparts on a diverse suite of tasks. We additionally introduce Flow-RBC, a new single-cell dataset and real-world application of permutation invariant prediction. We open-source our data and code here: https://github.com/rajesh-lab/deep_permutation_invariant.

Time Adaptive Gaussian Model

Multivariate time series analysis is becoming an integral part of data analysis pipelines. Understanding the individual time point connections between covariates as well as how these connections change in time is non-trivial. To this aim, we propose a novel method that leverages on Hidden Markov Models and Gaussian Graphical Models -- Time Adaptive Gaussian Model (TAGM). Our model is a generalization of state-of-the-art methods for the inference of temporal graphical models, its formulation leverages on both aspects of these models providing better results than current methods. In particular,it performs pattern recognition by clustering data points in time; and, it finds probabilistic (and possibly causal) relationships among the observed variables. Compared to current methods for temporal network inference, it reduces the basic assumptions while still showing good inference performances.

Group induced graphical lasso allows for discovery of molecular pathways-pathways interactions

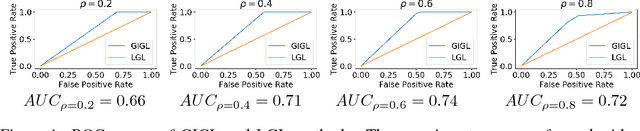
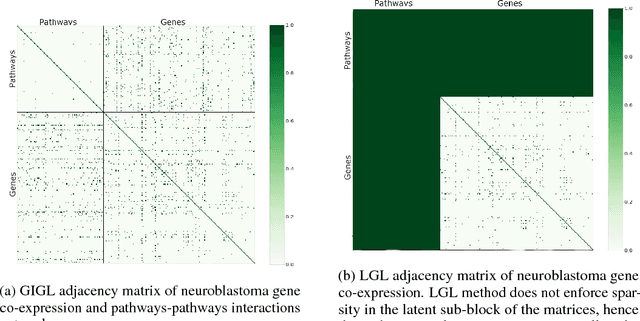
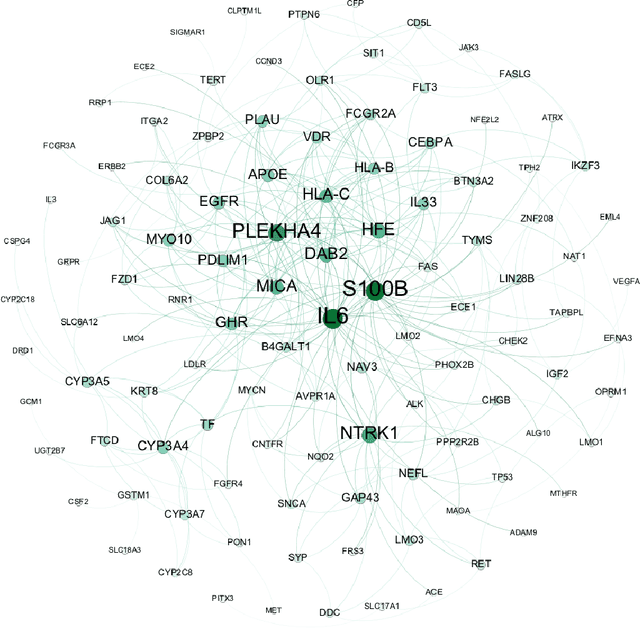
Complex systems may contain heterogeneous types of variables that interact in a multi-level and multi-scale manner. In this context, high-level layers may considered as groups of variables interacting in lower-level layers. This is particularly true in biology, where, for example, genes are grouped in pathways and two types of interactions are present: pathway-pathway interactions and gene-gene interactions. However, from data it is only possible to measure the expression of genes while it is impossible to directly measure the activity of pathways. Nevertheless, the knowledge on the inter-dependence between the groups and the variables allows for a multi-layer network inference, on both observed variables and groups, even if no direct information on the latter is present in the data (hence groups are considered as latent). In this paper, we propose an extension of the latent graphical lasso method that leverages on the knowledge of the inter-links between the hidden (groups) and observed layers. The method exploits the knowledge of group structure that influence the behaviour of observed variables to retrieve a two layers network. Its efficacy was tested on synthetic data to check its ability in retrieving the network structure compared to the ground truth. We present a case study on Neuroblastoma, which shows how our multi-level inference is relevant in real contexts to infer biologically meaningful connections.

Latent Variable Time-varying Network Inference

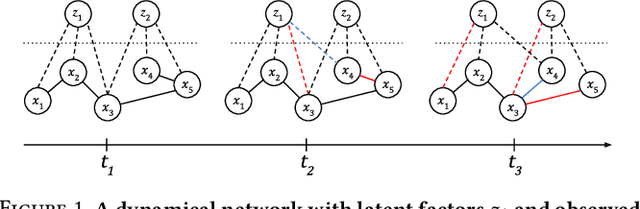
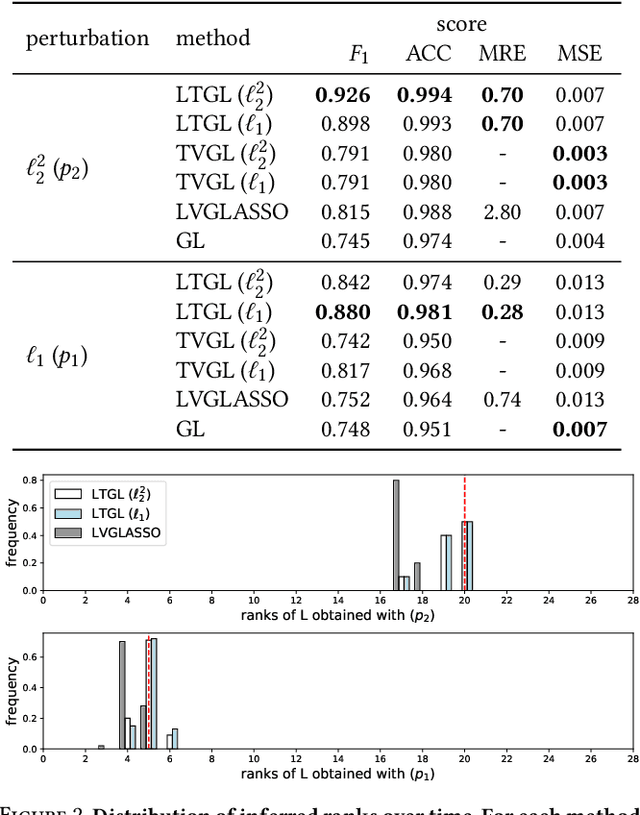
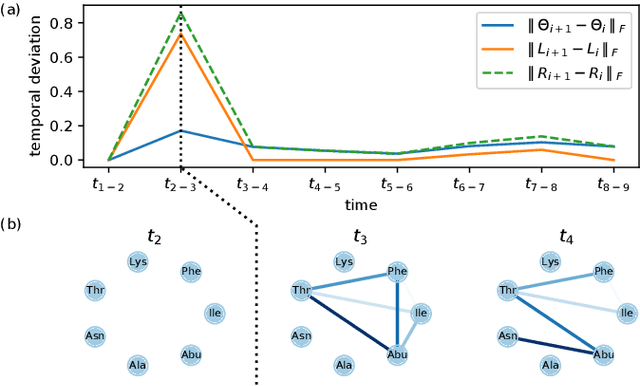
In many applications of finance, biology and sociology, complex systems involve entities interacting with each other. These processes have the peculiarity of evolving over time and of comprising latent factors, which influence the system without being explicitly measured. In this work we present latent variable time-varying graphical lasso (LTGL), a method for multivariate time-series graphical modelling that considers the influence of hidden or unmeasurable factors. The estimation of the contribution of the latent factors is embedded in the model which produces both sparse and low-rank components for each time point. In particular, the first component represents the connectivity structure of observable variables of the system, while the second represents the influence of hidden factors, assumed to be few with respect to the observed variables. Our model includes temporal consistency on both components, providing an accurate evolutionary pattern of the system. We derive a tractable optimisation algorithm based on alternating direction method of multipliers, and develop a scalable and efficient implementation which exploits proximity operators in closed form. LTGL is extensively validated on synthetic data, achieving optimal performance in terms of accuracy, structure learning and scalability with respect to ground truth and state-of-the-art methods for graphical inference. We conclude with the application of LTGL to real case studies, from biology and finance, to illustrate how our method can be successfully employed to gain insights on multivariate time-series data.