Margherita Squillario
Group induced graphical lasso allows for discovery of molecular pathways-pathways interactions
Nov 21, 2018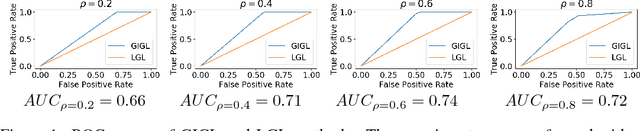

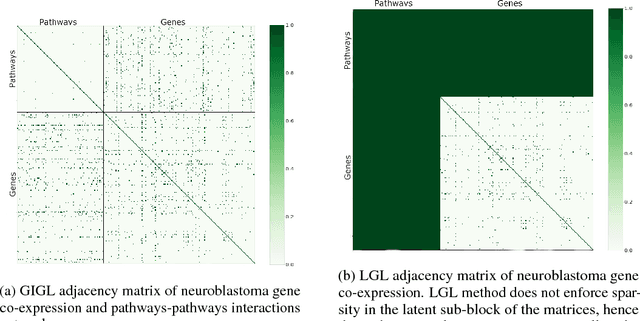
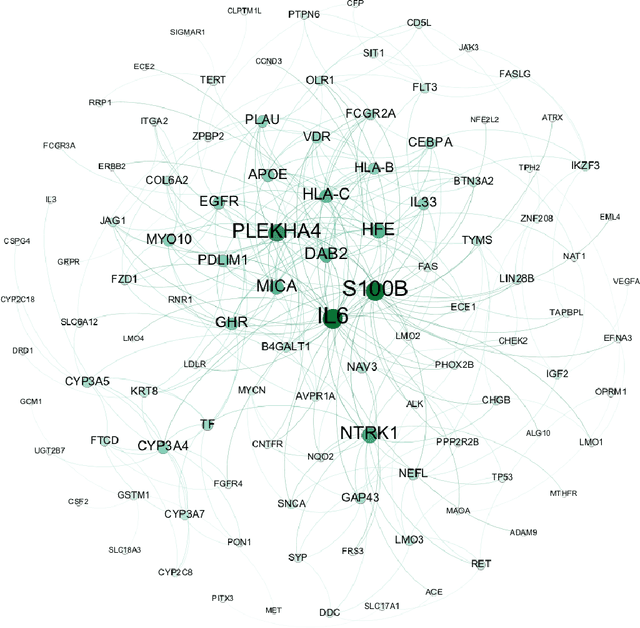
Abstract:Complex systems may contain heterogeneous types of variables that interact in a multi-level and multi-scale manner. In this context, high-level layers may considered as groups of variables interacting in lower-level layers. This is particularly true in biology, where, for example, genes are grouped in pathways and two types of interactions are present: pathway-pathway interactions and gene-gene interactions. However, from data it is only possible to measure the expression of genes while it is impossible to directly measure the activity of pathways. Nevertheless, the knowledge on the inter-dependence between the groups and the variables allows for a multi-layer network inference, on both observed variables and groups, even if no direct information on the latter is present in the data (hence groups are considered as latent). In this paper, we propose an extension of the latent graphical lasso method that leverages on the knowledge of the inter-links between the hidden (groups) and observed layers. The method exploits the knowledge of group structure that influence the behaviour of observed variables to retrieve a two layers network. Its efficacy was tested on synthetic data to check its ability in retrieving the network structure compared to the ground truth. We present a case study on Neuroblastoma, which shows how our multi-level inference is relevant in real contexts to infer biologically meaningful connections.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge