Latent Variable Time-varying Network Inference
Paper and Code
Aug 02, 2018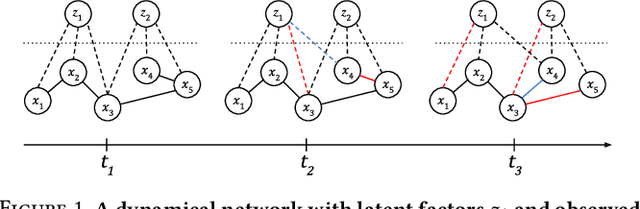
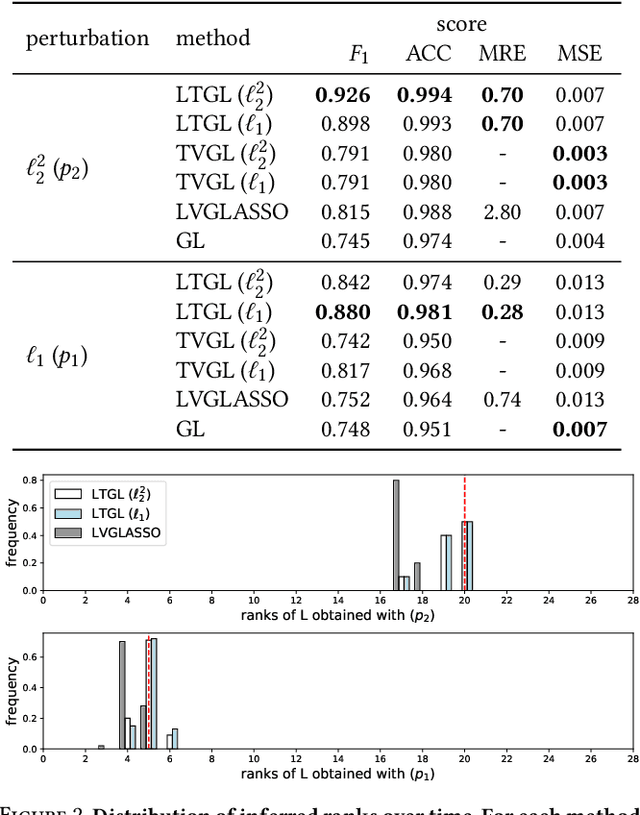

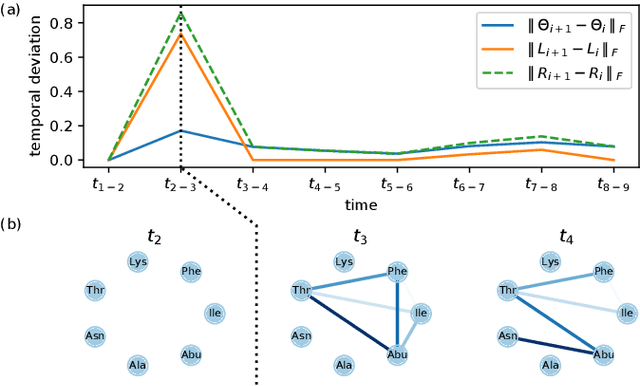
In many applications of finance, biology and sociology, complex systems involve entities interacting with each other. These processes have the peculiarity of evolving over time and of comprising latent factors, which influence the system without being explicitly measured. In this work we present latent variable time-varying graphical lasso (LTGL), a method for multivariate time-series graphical modelling that considers the influence of hidden or unmeasurable factors. The estimation of the contribution of the latent factors is embedded in the model which produces both sparse and low-rank components for each time point. In particular, the first component represents the connectivity structure of observable variables of the system, while the second represents the influence of hidden factors, assumed to be few with respect to the observed variables. Our model includes temporal consistency on both components, providing an accurate evolutionary pattern of the system. We derive a tractable optimisation algorithm based on alternating direction method of multipliers, and develop a scalable and efficient implementation which exploits proximity operators in closed form. LTGL is extensively validated on synthetic data, achieving optimal performance in terms of accuracy, structure learning and scalability with respect to ground truth and state-of-the-art methods for graphical inference. We conclude with the application of LTGL to real case studies, from biology and finance, to illustrate how our method can be successfully employed to gain insights on multivariate time-series data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge