A Neural Framework for Learning Subgraph and Graph Similarity Measures

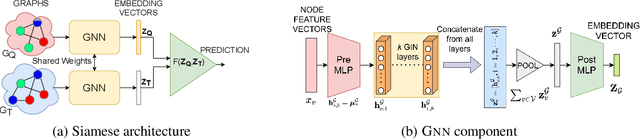
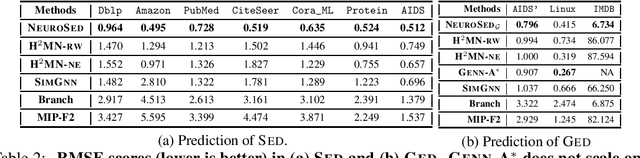
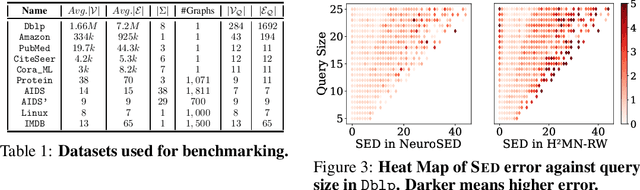
Subgraph similarity search is a fundamental operator in graph analysis. In this framework, given a query graph and a graph database, the goal is to identify subgraphs of the database graphs that are structurally similar to the query. Subgraph edit distance (SED) is one of the most expressive measures for subgraph similarity. In this work, we study the problem of learning SED from a training set of graph pairs and their SED values. Towards that end, we design a novel siamese graph neural network called NEUROSED, which learns an embedding space with a rich structure reminiscent of SED. With the help of a specially crafted inductive bias, NEUROSED not only enables high accuracy but also ensures that the predicted SED, like true SED, satisfies triangle inequality. The design is generic enough to also model graph edit distance (GED), while ensuring that the predicted GED space is metric, like the true GED space. Extensive experiments on real graph datasets, for both SED and GED, establish that NEUROSED achieves approximately 2 times lower RMSE than the state of the art and is approximately 18 times faster than the fastest baseline. Further, owing to its pair-independent embeddings and theoretical properties, NEUROSED allows approximately 3 orders of magnitude faster retrieval of graphs and subgraphs.

PoWER-BERT: Accelerating BERT inference for Classification Tasks

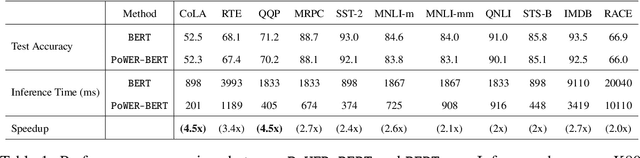
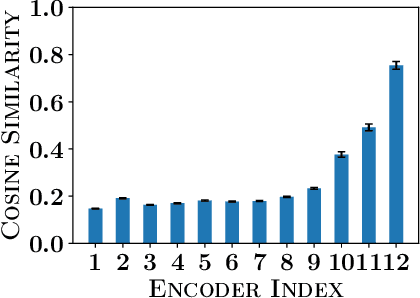
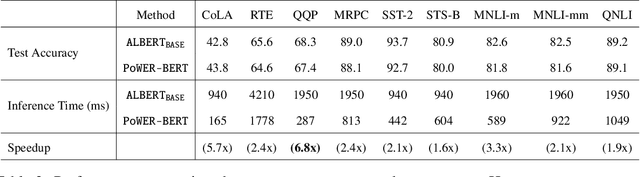
BERT has emerged as a popular model for natural language understanding. Given its compute intensive nature, even for inference, many recent studies have considered optimization of two important performance characteristics: model size and inference time. We consider classification tasks and propose a novel method, called PoWER-BERT, for improving the inference time for the BERT model without significant loss in the accuracy. The method works by eliminating word-vectors (intermediate vector outputs) from the encoder pipeline. We design a strategy for measuring the significance of the word-vectors based on the self-attention mechanism of the encoders which helps us identify the word-vectors to be eliminated. Experimental evaluation on the standard GLUE benchmark shows that PoWER-BERT achieves up to 4.5x reduction in inference time over BERT with < 1% loss in accuracy. We show that compared to the prior inference time reduction methods, PoWER-BERT offers better trade-off between accuracy and inference time. Lastly, we demonstrate that our scheme can also be used in conjunction with ALBERT (a highly compressed version of BERT) and can attain up to 6.8x factor reduction in inference time with < 1% loss in accuracy.