Siddharth Grover
A Neural Framework for Learning Subgraph and Graph Similarity Measures
Dec 28, 2021
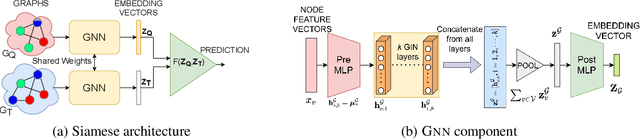
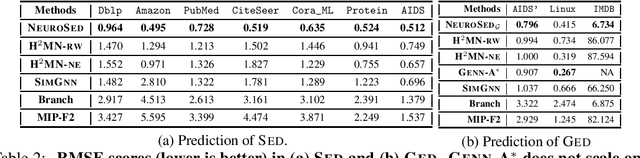
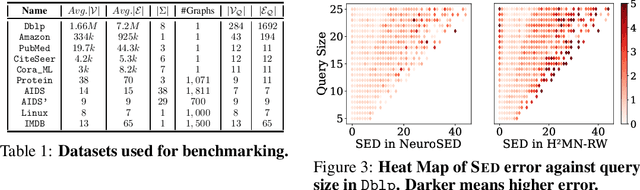
Abstract:Subgraph similarity search is a fundamental operator in graph analysis. In this framework, given a query graph and a graph database, the goal is to identify subgraphs of the database graphs that are structurally similar to the query. Subgraph edit distance (SED) is one of the most expressive measures for subgraph similarity. In this work, we study the problem of learning SED from a training set of graph pairs and their SED values. Towards that end, we design a novel siamese graph neural network called NEUROSED, which learns an embedding space with a rich structure reminiscent of SED. With the help of a specially crafted inductive bias, NEUROSED not only enables high accuracy but also ensures that the predicted SED, like true SED, satisfies triangle inequality. The design is generic enough to also model graph edit distance (GED), while ensuring that the predicted GED space is metric, like the true GED space. Extensive experiments on real graph datasets, for both SED and GED, establish that NEUROSED achieves approximately 2 times lower RMSE than the state of the art and is approximately 18 times faster than the fastest baseline. Further, owing to its pair-independent embeddings and theoretical properties, NEUROSED allows approximately 3 orders of magnitude faster retrieval of graphs and subgraphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge