When Less is More: 8-bit Quantization Improves Continual Learning in Large Language Models

Catastrophic forgetting poses a fundamental challenge in continual learning, particularly when models are quantized for deployment efficiency. We systematically investigate the interplay between quantization precision (FP16, INT8, INT4) and replay buffer strategies in large language models, revealing unexpected dynamics. While FP16 achieves superior initial task performance (74.44% on NLU), we observe a striking inversion on subsequent tasks: quantized models outperform FP16 by 8-15% on final task forward accuracy, with INT4 achieving nearly double FP16's performance on Code generation (40% vs 20%). Critically, even minimal replay buffers (0.1%) dramatically improve retention - increasing NLU retention after Math training from 45% to 65% across all precision levels - with INT8 consistently achieving the optimal balance between learning plasticity and knowledge retention. We hypothesize that quantization-induced noise acts as implicit regularization, preventing the overfitting to new task gradients that plagues high-precision models. These findings challenge the conventional wisdom that higher precision is always preferable, suggesting instead that INT8 quantization offers both computational efficiency and superior continual learning dynamics. Our results provide practical guidelines for deploying compressed models in continual learning scenarios: small replay buffers (1-2%) suffice for NLU tasks, while Math and Code benefit from moderate buffers (5-10%), with quantized models requiring less replay than FP16 to achieve comparable retention. Code is available at https://github.com/Festyve/LessIsMore.

GamiBench: Evaluating Spatial Reasoning and 2D-to-3D Planning Capabilities of MLLMs with Origami Folding Tasks

Multimodal large language models (MLLMs) are proficient in perception and instruction-following, but they still struggle with spatial reasoning: the ability to mentally track and manipulate objects across multiple views and over time. Spatial reasoning is a key component of human intelligence, but most existing benchmarks focus on static images or final outputs, failing to account for the sequential and viewpoint-dependent nature of this skill. To close this gap, we introduce GamiBench, a benchmark designed to evaluate spatial reasoning and 2D-to-3D planning in MLLMs through origami-inspired folding tasks. GamiBench includes 186 regular and 186 impossible 2D crease patterns paired with their corresponding 3D folded shapes, produced from six distinct viewpoints across three visual question-answering (VQA) tasks: predicting 3D fold configurations, distinguishing valid viewpoints, and detecting impossible patterns. Unlike previous benchmarks that assess only final predictions, GamiBench holistically evaluates the entire reasoning process--measuring cross-view consistency, physical feasibility through impossible-fold detection, and interpretation of intermediate folding steps. It further introduces new diagnostic metrics--viewpoint consistency (VC) and impossible fold selection rate (IFSR)--to measure how well models handle folds of varying complexity. Our experiments show that even leading models such as GPT-5 and Gemini-2.5-Pro struggle on single-step spatial understanding. These contributions establish a standardized framework for evaluating geometric understanding and spatial reasoning in MLLMs. Dataset and code: https://github.com/stvngo/GamiBench.

Enhanced Survival Prediction in Head and Neck Cancer Using Convolutional Block Attention and Multimodal Data Fusion

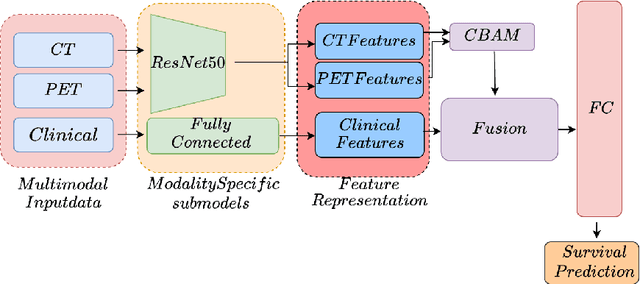
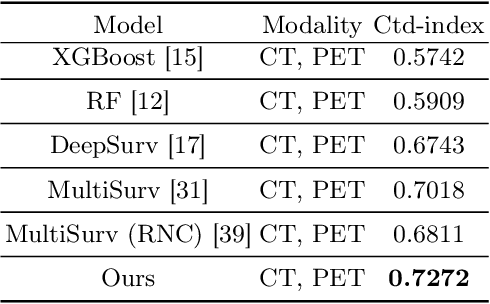
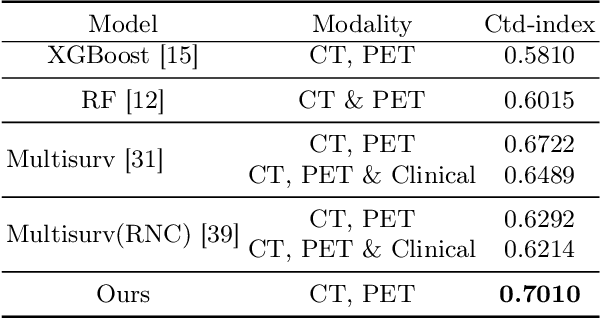
Accurate survival prediction in head and neck cancer (HNC) is essential for guiding clinical decision-making and optimizing treatment strategies. Traditional models, such as Cox proportional hazards, have been widely used but are limited in their ability to handle complex multi-modal data. This paper proposes a deep learning-based approach leveraging CT and PET imaging modalities to predict survival outcomes in HNC patients. Our method integrates feature extraction with a Convolutional Block Attention Module (CBAM) and a multi-modal data fusion layer that combines imaging data to generate a compact feature representation. The final prediction is achieved through a fully parametric discrete-time survival model, allowing for flexible hazard functions that overcome the limitations of traditional survival models. We evaluated our approach using the HECKTOR and HEAD-NECK-RADIOMICS- HN1 datasets, demonstrating its superior performance compared to conconventional statistical and machine learning models. The results indicate that our deep learning model significantly improves survival prediction accuracy, offering a robust tool for personalized treatment planning in HNC

PalmBench: A Comprehensive Benchmark of Compressed Large Language Models on Mobile Platforms

Deploying large language models (LLMs) locally on mobile devices is advantageous in scenarios where transmitting data to remote cloud servers is either undesirable due to privacy concerns or impractical due to network connection. Recent advancements (MLC, 2023a; Gerganov, 2023) have facilitated the local deployment of LLMs. However, local deployment also presents challenges, particularly in balancing quality (generative performance), latency, and throughput within the hardware constraints of mobile devices. In this paper, we introduce our lightweight, all-in-one automated benchmarking framework that allows users to evaluate LLMs on mobile devices. We provide a comprehensive benchmark of various popular LLMs with different quantization configurations (both weights and activations) across multiple mobile platforms with varying hardware capabilities. Unlike traditional benchmarks that assess full-scale models on high-end GPU clusters, we focus on evaluating resource efficiency (memory and power consumption) and harmful output for compressed models on mobile devices. Our key observations include i) differences in energy efficiency and throughput across mobile platforms; ii) the impact of quantization on memory usage, GPU execution time, and power consumption; and iii) accuracy and performance degradation of quantized models compared to their non-quantized counterparts; and iv) the frequency of hallucinations and toxic content generated by compressed LLMs on mobile devices.

Explaining Neural Scaling Laws

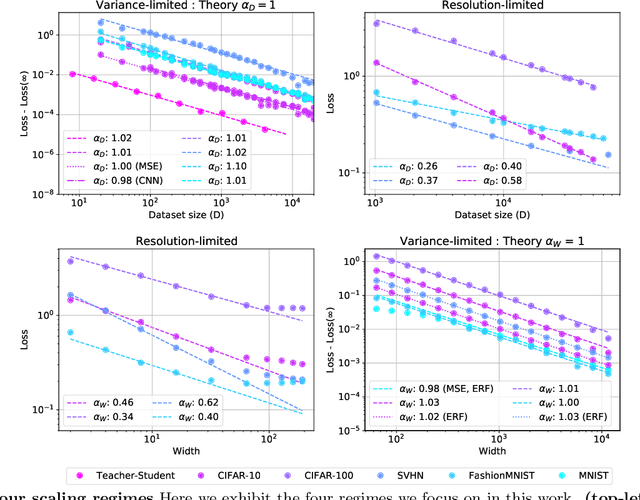
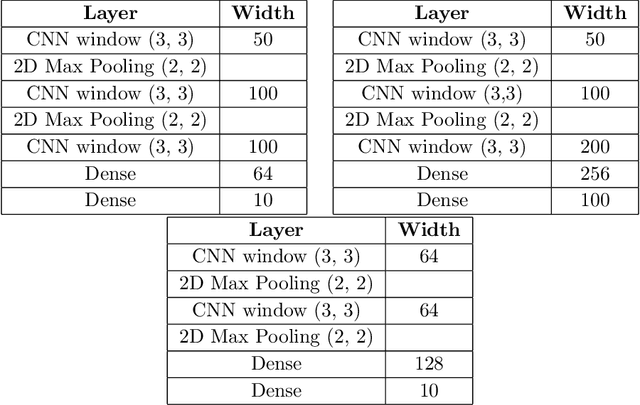
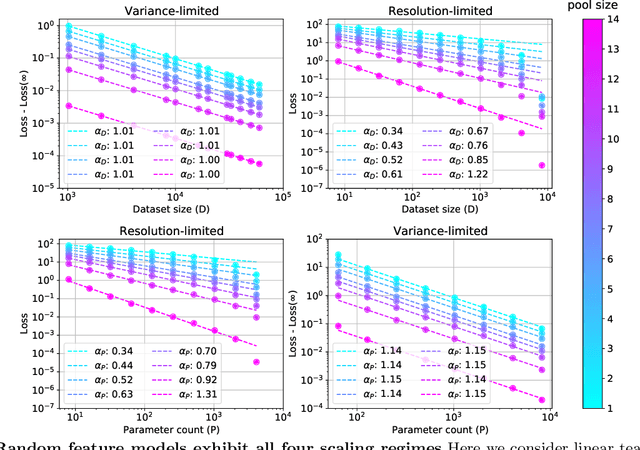
The test loss of well-trained neural networks often follows precise power-law scaling relations with either the size of the training dataset or the number of parameters in the network. We propose a theory that explains and connects these scaling laws. We identify variance-limited and resolution-limited scaling behavior for both dataset and model size, for a total of four scaling regimes. The variance-limited scaling follows simply from the existence of a well-behaved infinite data or infinite width limit, while the resolution-limited regime can be explained by positing that models are effectively resolving a smooth data manifold. In the large width limit, this can be equivalently obtained from the spectrum of certain kernels, and we present evidence that large width and large dataset resolution-limited scaling exponents are related by a duality. We exhibit all four scaling regimes in the controlled setting of large random feature and pretrained models and test the predictions empirically on a range of standard architectures and datasets. We also observe several empirical relationships between datasets and scaling exponents: super-classing image tasks does not change exponents, while changing input distribution (via changing datasets or adding noise) has a strong effect. We further explore the effect of architecture aspect ratio on scaling exponents.

A Neural Scaling Law from the Dimension of the Data Manifold

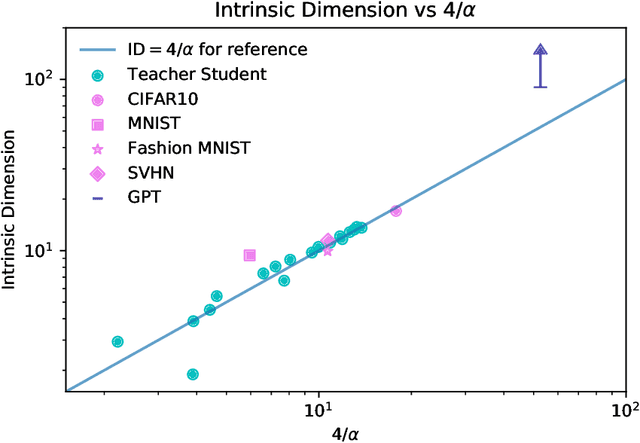
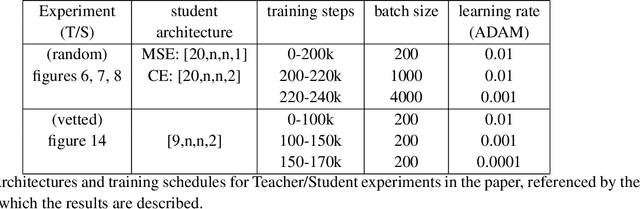
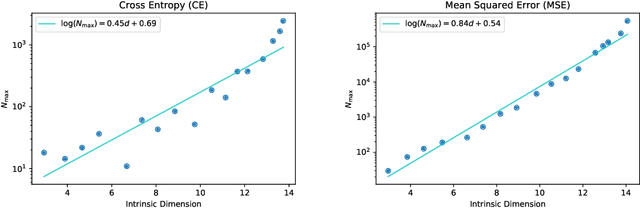
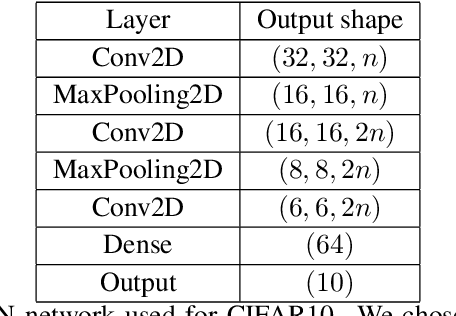
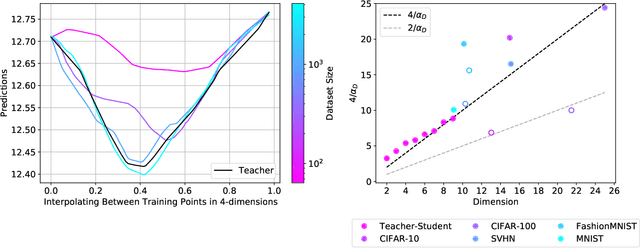
When data is plentiful, the loss achieved by well-trained neural networks scales as a power-law $L \propto N^{-\alpha}$ in the number of network parameters $N$. This empirical scaling law holds for a wide variety of data modalities, and may persist over many orders of magnitude. The scaling law can be explained if neural models are effectively just performing regression on a data manifold of intrinsic dimension $d$. This simple theory predicts that the scaling exponents $\alpha \approx 4/d$ for cross-entropy and mean-squared error losses. We confirm the theory by independently measuring the intrinsic dimension and the scaling exponents in a teacher/student framework, where we can study a variety of $d$ and $\alpha$ by dialing the properties of random teacher networks. We also test the theory with CNN image classifiers on several datasets and with GPT-type language models.