Model-Based Inference and Experimental Design for Interference Using Partial Network Data

The stable unit treatment value assumption states that the outcome of an individual is not affected by the treatment statuses of others, however in many real world applications, treatments can have an effect on many others beyond the immediately treated. Interference can generically be thought of as mediated through some network structure. In many empirically relevant situations however, complete network data (required to adjust for these spillover effects) are too costly or logistically infeasible to collect. Partially or indirectly observed network data (e.g., subsamples, aggregated relational data (ARD), egocentric sampling, or respondent-driven sampling) reduce the logistical and financial burden of collecting network data, but the statistical properties of treatment effect adjustments from these design strategies are only beginning to be explored. In this paper, we present a framework for the estimation and inference of treatment effect adjustments using partial network data through the lens of structural causal models. We also illustrate procedures to assign treatments using only partial network data, with the goal of either minimizing estimator variance or optimally seeding. We derive single network asymptotic results applicable to a variety of choices for an underlying graph model. We validate our approach using simulated experiments on observed graphs with applications to information diffusion in India and Malawi.

From Narratives to Numbers: Valid Inference Using Language Model Predictions from Verbal Autopsy Narratives

In settings where most deaths occur outside the healthcare system, verbal autopsies (VAs) are a common tool to monitor trends in causes of death (COD). VAs are interviews with a surviving caregiver or relative that are used to predict the decedent's COD. Turning VAs into actionable insights for researchers and policymakers requires two steps (i) predicting likely COD using the VA interview and (ii) performing inference with predicted CODs (e.g. modeling the breakdown of causes by demographic factors using a sample of deaths). In this paper, we develop a method for valid inference using outcomes (in our case COD) predicted from free-form text using state-of-the-art NLP techniques. This method, which we call multiPPI++, extends recent work in "prediction-powered inference" to multinomial classification. We leverage a suite of NLP techniques for COD prediction and, through empirical analysis of VA data, demonstrate the effectiveness of our approach in handling transportability issues. multiPPI++ recovers ground truth estimates, regardless of which NLP model produced predictions and regardless of whether they were produced by a more accurate predictor like GPT-4-32k or a less accurate predictor like KNN. Our findings demonstrate the practical importance of inference correction for public health decision-making and suggests that if inference tasks are the end goal, having a small amount of contextually relevant, high quality labeled data is essential regardless of the NLP algorithm.

Robustly estimating heterogeneity in factorial data using Rashomon Partitions

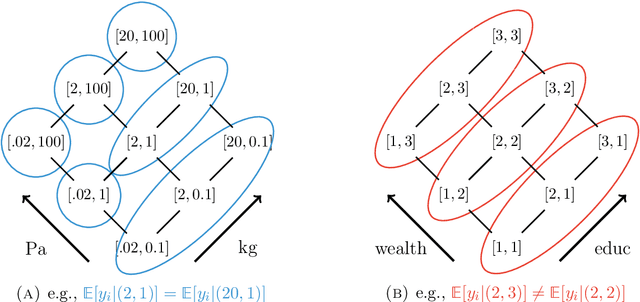
Many statistical analyses, in both observational data and randomized control trials, ask: how does the outcome of interest vary with combinations of observable covariates? How do various drug combinations affect health outcomes, or how does technology adoption depend on incentives and demographics? Our goal is to partition this factorial space into ``pools'' of covariate combinations where the outcome differs across the pools (but not within a pool). Existing approaches (i) search for a single ``optimal'' partition under assumptions about the association between covariates or (ii) sample from the entire set of possible partitions. Both these approaches ignore the reality that, especially with correlation structure in covariates, many ways to partition the covariate space may be statistically indistinguishable, despite very different implications for policy or science. We develop an alternative perspective, called Rashomon Partition Sets (RPSs). Each item in the RPS partitions the space of covariates using a tree-like geometry. RPSs incorporate all partitions that have posterior values near the maximum a posteriori partition, even if they offer substantively different explanations, and do so using a prior that makes no assumptions about associations between covariates. This prior is the $\ell_0$ prior, which we show is minimax optimal. Given the RPS we calculate the posterior of any measurable function of the feature effects vector on outcomes, conditional on being in the RPS. We also characterize approximation error relative to the entire posterior and provide bounds on the size of the RPS. Simulations demonstrate this framework allows for robust conclusions relative to conventional regularization techniques. We apply our method to three empirical settings: price effects on charitable giving, chromosomal structure (telomere length), and the introduction of microfinance.

Do We Really Even Need Data?

As artificial intelligence and machine learning tools become more accessible, and scientists face new obstacles to data collection (e.g. rising costs, declining survey response rates), researchers increasingly use predictions from pre-trained algorithms as outcome variables. Though appealing for financial and logistical reasons, using standard tools for inference can misrepresent the association between independent variables and the outcome of interest when the true, unobserved outcome is replaced by a predicted value. In this paper, we characterize the statistical challenges inherent to this so-called ``inference with predicted data'' problem and elucidate three potential sources of error: (i) the relationship between predicted outcomes and their true, unobserved counterparts, (ii) robustness of the machine learning model to resampling or uncertainty about the training data, and (iii) appropriately propagating not just bias but also uncertainty from predictions into the ultimate inference procedure.

Bayesian Hyperbolic Multidimensional Scaling

Multidimensional scaling (MDS) is a widely used approach to representing high-dimensional, dependent data. MDS works by assigning each observation a location on a low-dimensional geometric manifold, with distance on the manifold representing similarity. We propose a Bayesian approach to multidimensional scaling when the low-dimensional manifold is hyperbolic. Using hyperbolic space facilitates representing tree-like structure common in many settings (e.g. text or genetic data with hierarchical structure). A Bayesian approach provides regularization that minimizes the impact of uncertainty or measurement error in the observed data. We also propose a case-control likelihood approximation that allows for efficient sampling from the posterior in larger data settings, reducing computational complexity from approximately $O(n^2)$ to $O(n)$. We evaluate the proposed method against state-of-the-art alternatives using simulations, canonical reference datasets, and human gene expression data.

Spectral goodness-of-fit tests for complete and partial network data

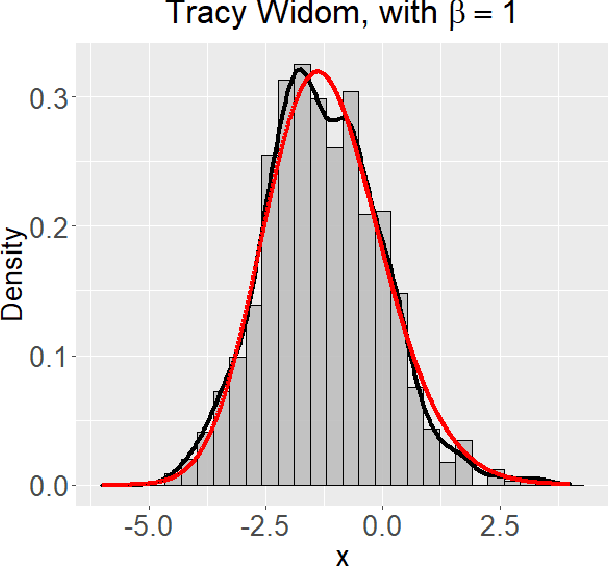
Networks describe the, often complex, relationships between individual actors. In this work, we address the question of how to determine whether a parametric model, such as a stochastic block model or latent space model, fits a dataset well and will extrapolate to similar data. We use recent results in random matrix theory to derive a general goodness-of-fit test for dyadic data. We show that our method, when applied to a specific model of interest, provides an straightforward, computationally fast way of selecting parameters in a number of commonly used network models. For example, we show how to select the dimension of the latent space in latent space models. Unlike other network goodness-of-fit methods, our general approach does not require simulating from a candidate parametric model, which can be cumbersome with large graphs, and eliminates the need to choose a particular set of statistics on the graph for comparison. It also allows us to perform goodness-of-fit tests on partial network data, such as Aggregated Relational Data. We show with simulations that our method performs well in many situations of interest. We analyze several empirically relevant networks and show that our method leads to improved community detection algorithms. R code to implement our method is available on Github.

Inference for Network Regression Models with Community Structure

Network regression models, where the outcome comprises the valued edge in a network and the predictors are actor or dyad-level covariates, are used extensively in the social and biological sciences. Valid inference relies on accurately modeling the residual dependencies among the relations. Frequently homogeneity assumptions are placed on the errors which are commonly incorrect and ignore critical, natural clustering of the actors. In this work, we present a novel regression modeling framework that models the errors as resulting from a community-based dependence structure and exploits the subsequent exchangeability properties of the error distribution to obtain parsimonious standard errors for regression parameters.

Identifying the latent space geometry of network models through analysis of curvature

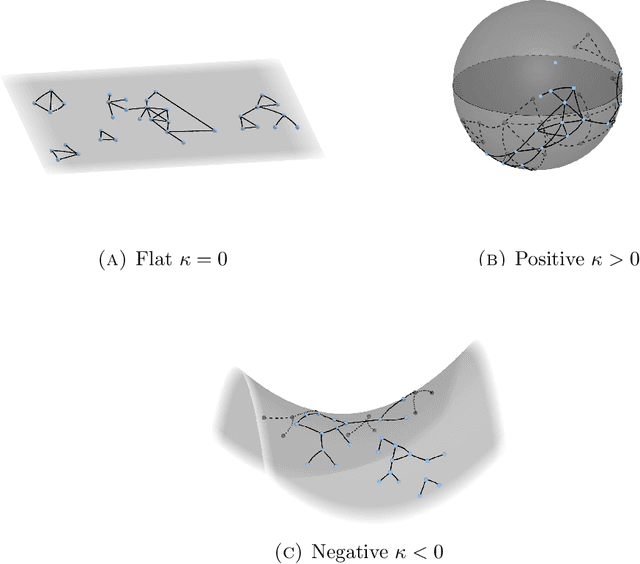
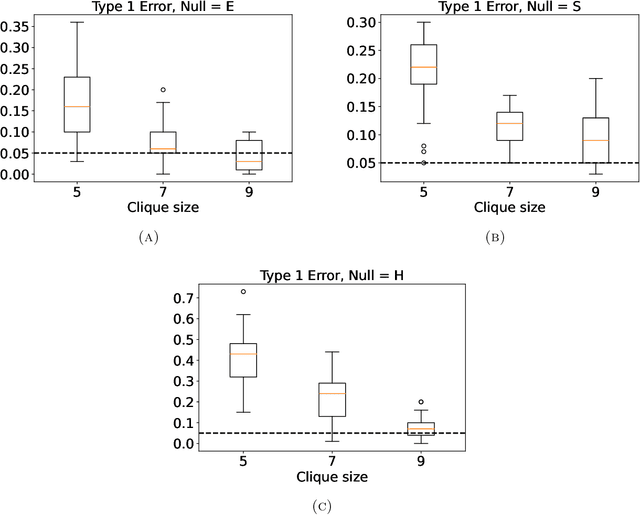
Statistically modeling networks, across numerous disciplines and contexts, is fundamentally challenging because of (often high-order) dependence between connections. A common approach assigns each person in the graph to a position on a low-dimensional manifold. Distance between individuals in this (latent) space is inversely proportional to the likelihood of forming a connection. The choice of the latent geometry (the manifold class, dimension, and curvature) has consequential impacts on the substantive conclusions of the model. More positive curvature in the manifold, for example, encourages more and tighter communities; negative curvature induces repulsion among nodes. Currently, however, the choice of the latent geometry is an a priori modeling assumption and there is limited guidance about how to make these choices in a data-driven way. In this work, we present a method to consistently estimate the manifold type, dimension, and curvature from an empirically relevant class of latent spaces: simply connected, complete Riemannian manifolds of constant curvature. Our core insight comes by representing the graph as a noisy distance matrix based on the ties between cliques. Leveraging results from statistical geometry, we develop hypothesis tests to determine whether the observed distances could plausibly be embedded isometrically in each of the candidate geometries. We explore the accuracy of our approach with simulations and then apply our approach to data-sets from economics and sociology as well as neuroscience.

Anomaly Detection in Large Scale Networks with Latent Space Models

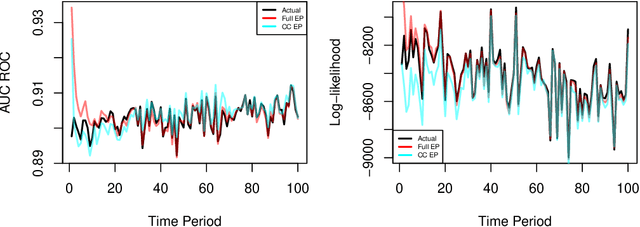
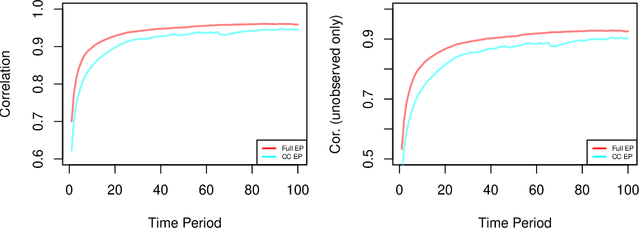
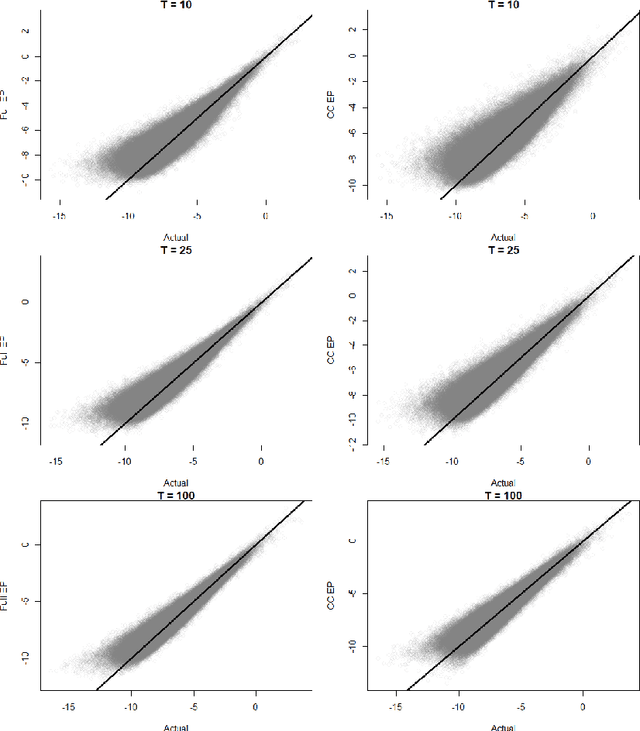
We develop a real-time anomaly detection algorithm for directed activity on large, sparse networks. We model the propensity for future activity using a dynamic logistic model with interaction terms for sender- and receiver-specific latent factors in addition to sender- and receiver-specific popularity scores; deviations from this underlying model constitute potential anomalies. Latent nodal attributes are estimated via a variational Bayesian approach and may change over time, representing natural shifts in network activity. Estimation is augmented with a case-control approximation to take advantage of the sparsity of the network and reduces computational complexity from $O(N^2)$ to $O(E)$, where $N$ is the number of nodes and $E$ is the number of observed edges. We run our algorithm on network event records collected from an enterprise network of over 25,000 computers and are able to identify a red team attack with half the detection rate required of the model without latent interaction terms.

An Expectation Conditional Maximization approach for Gaussian graphical models

Bayesian graphical models are a useful tool for understanding dependence relationships among many variables, particularly in situations with external prior information. In high-dimensional settings, the space of possible graphs becomes enormous, rendering even state-of-the-art Bayesian stochastic search computationally infeasible. We propose a deterministic alternative to estimate Gaussian and Gaussian copula graphical models using an Expectation Conditional Maximization (ECM) algorithm, extending the EM approach from Bayesian variable selection to graphical model estimation. We show that the ECM approach enables fast posterior exploration under a sequence of mixture priors, and can incorporate multiple sources of information.