Process-Supervised Reward Models for Clinical Note Generation: A Scalable Approach Guided by Domain Expertise

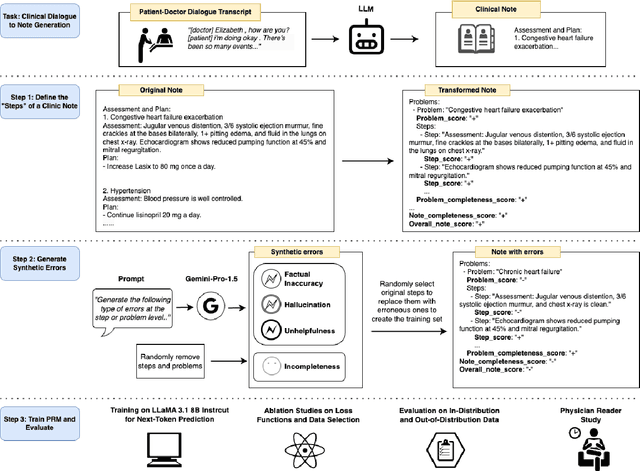
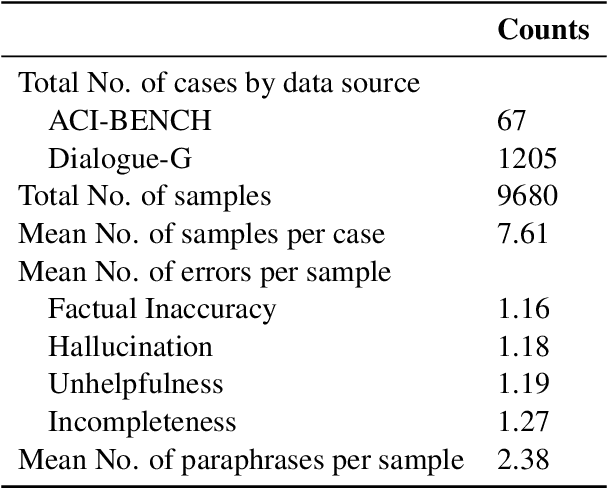
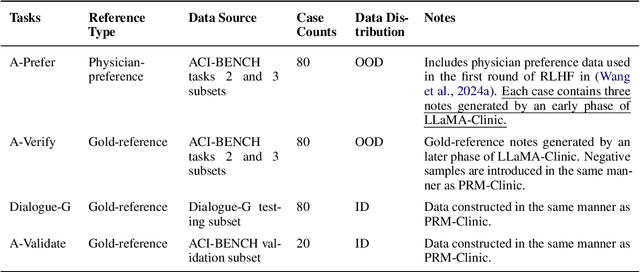
Process-supervised reward models (PRMs), which verify large language model (LLM) outputs step-by-step, have achieved significant success in mathematical and coding problems. However, their application to other domains remains largely unexplored. In this work, we train a PRM to provide step-level reward signals for clinical notes generated by LLMs from patient-doctor dialogues. Guided by real-world clinician expertise, we carefully designed step definitions for clinical notes and utilized Gemini-Pro 1.5 to automatically generate process supervision data at scale. Our proposed PRM, trained on the LLaMA-3.1 8B instruct model, demonstrated superior performance compared to Gemini-Pro 1.5 and an outcome-supervised reward model (ORM) across two key evaluations: (1) the accuracy of selecting gold-reference samples from error-containing samples, achieving 98.8% (versus 61.3% for ORM and 93.8% for Gemini-Pro 1.5), and (2) the accuracy of selecting physician-preferred notes, achieving 56.2% (compared to 51.2% for ORM and 50.0% for Gemini-Pro 1.5). Additionally, we conducted ablation studies to determine optimal loss functions and data selection strategies, along with physician reader studies to explore predictors of downstream Best-of-N performance. Our promising results suggest the potential of PRMs to extend beyond the clinical domain, offering a scalable and effective solution for diverse generative tasks.

Towards Adapting Open-Source Large Language Models for Expert-Level Clinical Note Generation

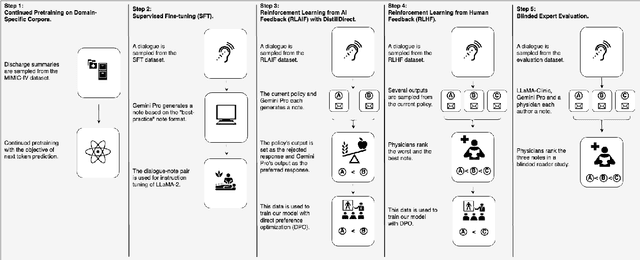
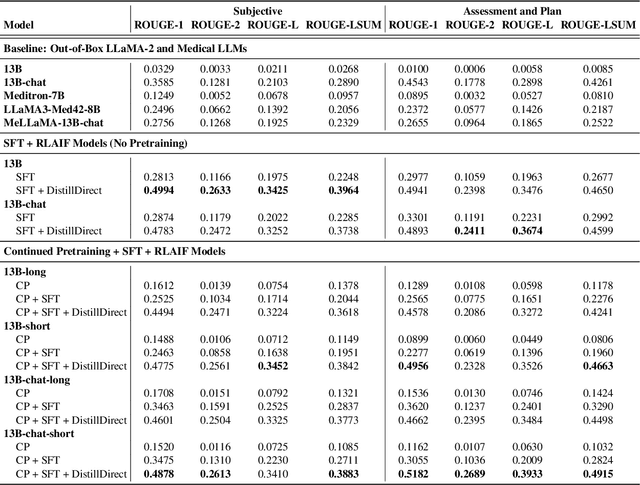
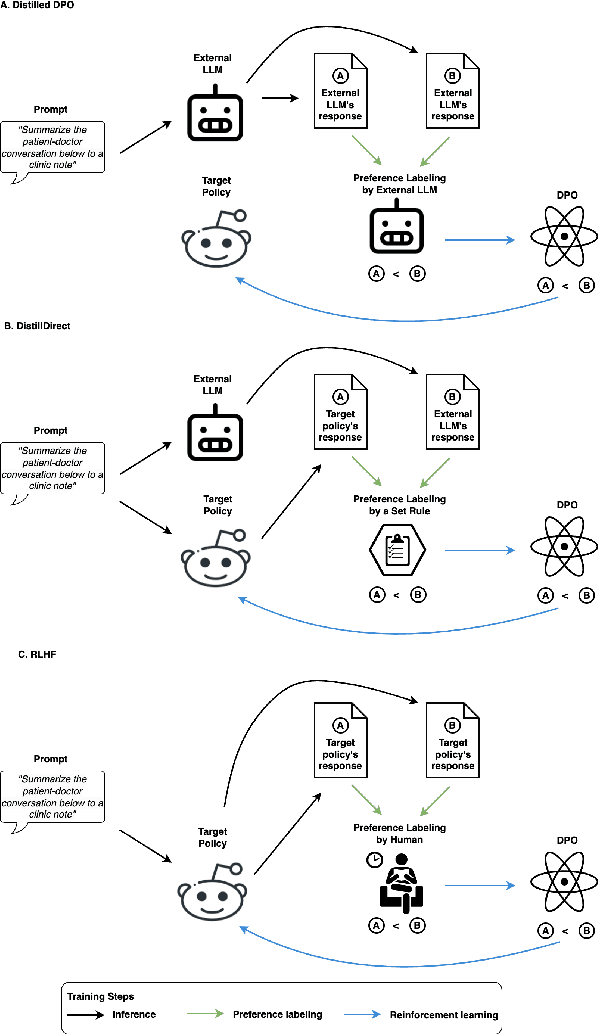
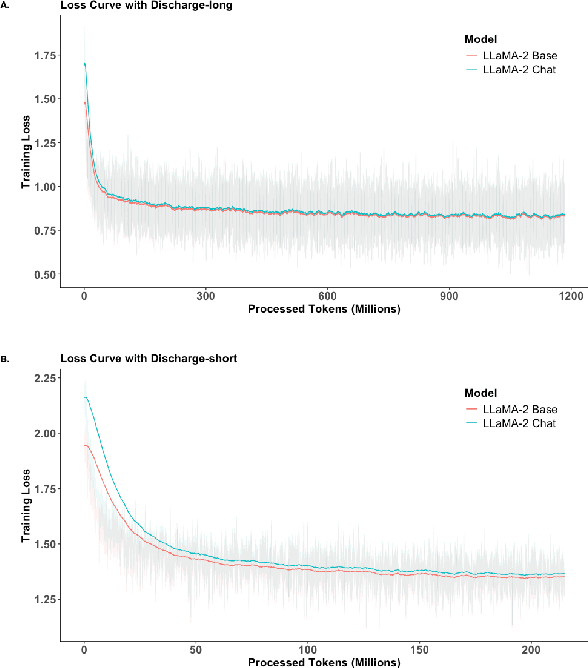
Large Language Models (LLMs) have shown promising capabilities in handling clinical text summarization tasks. In this study, we demonstrate that a small open-source LLM can be effectively trained to generate high-quality clinical notes from outpatient patient-doctor dialogues. We achieve this through a comprehensive domain- and task-specific adaptation process for the LLaMA-2 13 billion parameter model. This process incorporates continued pre-training, supervised fine-tuning, and reinforcement learning from both AI and human feedback. We introduced an enhanced approach, termed DistillDirect, for performing on-policy reinforcement learning with Gemini Pro serving as the teacher model. Our resulting model, LLaMA-Clinic, is capable of generating clinical notes that are comparable in quality to those authored by physicians. In a blinded physician reader study, the majority (90.4%) of individual evaluations rated the notes generated by LLaMA-Clinic as "acceptable" or higher across all three criteria: real-world readiness, completeness, and accuracy. Notably, in the more challenging "Assessment and Plan" section, LLaMA-Clinic scored higher (4.2/5) in real-world readiness compared to physician-authored notes (4.1/5). Additionally, we identified caveats in public clinical note datasets, such as ACI-BENCH. We highlight key considerations for future clinical note-generation tasks, emphasizing the importance of pre-defining a best-practice note format. Overall, our research demonstrates the potential and feasibility of training smaller, open-source LLMs to assist with clinical documentation, capitalizing on healthcare institutions' access to patient records and domain expertise. We have made our newly created synthetic clinic dialogue-note dataset and the physician feedback dataset publicly available to foster future research in this field.

Bayesian Hyperbolic Multidimensional Scaling

Multidimensional scaling (MDS) is a widely used approach to representing high-dimensional, dependent data. MDS works by assigning each observation a location on a low-dimensional geometric manifold, with distance on the manifold representing similarity. We propose a Bayesian approach to multidimensional scaling when the low-dimensional manifold is hyperbolic. Using hyperbolic space facilitates representing tree-like structure common in many settings (e.g. text or genetic data with hierarchical structure). A Bayesian approach provides regularization that minimizes the impact of uncertainty or measurement error in the observed data. We also propose a case-control likelihood approximation that allows for efficient sampling from the posterior in larger data settings, reducing computational complexity from approximately $O(n^2)$ to $O(n)$. We evaluate the proposed method against state-of-the-art alternatives using simulations, canonical reference datasets, and human gene expression data.

Spectral goodness-of-fit tests for complete and partial network data

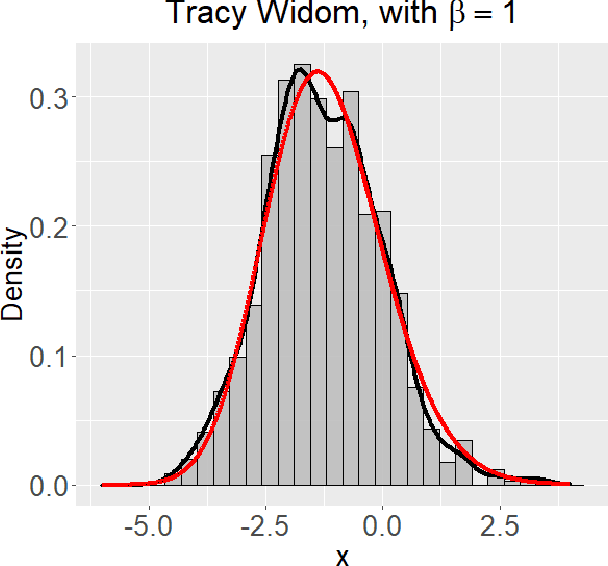
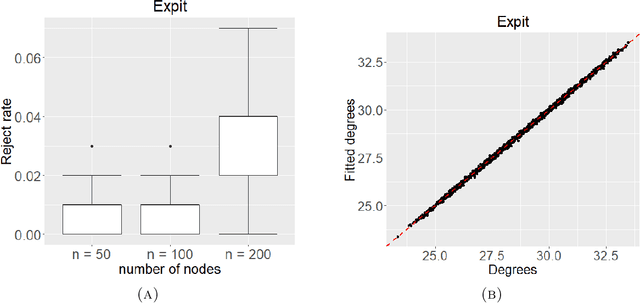
Networks describe the, often complex, relationships between individual actors. In this work, we address the question of how to determine whether a parametric model, such as a stochastic block model or latent space model, fits a dataset well and will extrapolate to similar data. We use recent results in random matrix theory to derive a general goodness-of-fit test for dyadic data. We show that our method, when applied to a specific model of interest, provides an straightforward, computationally fast way of selecting parameters in a number of commonly used network models. For example, we show how to select the dimension of the latent space in latent space models. Unlike other network goodness-of-fit methods, our general approach does not require simulating from a candidate parametric model, which can be cumbersome with large graphs, and eliminates the need to choose a particular set of statistics on the graph for comparison. It also allows us to perform goodness-of-fit tests on partial network data, such as Aggregated Relational Data. We show with simulations that our method performs well in many situations of interest. We analyze several empirically relevant networks and show that our method leads to improved community detection algorithms. R code to implement our method is available on Github.