Model-Based Inference and Experimental Design for Interference Using Partial Network Data

The stable unit treatment value assumption states that the outcome of an individual is not affected by the treatment statuses of others, however in many real world applications, treatments can have an effect on many others beyond the immediately treated. Interference can generically be thought of as mediated through some network structure. In many empirically relevant situations however, complete network data (required to adjust for these spillover effects) are too costly or logistically infeasible to collect. Partially or indirectly observed network data (e.g., subsamples, aggregated relational data (ARD), egocentric sampling, or respondent-driven sampling) reduce the logistical and financial burden of collecting network data, but the statistical properties of treatment effect adjustments from these design strategies are only beginning to be explored. In this paper, we present a framework for the estimation and inference of treatment effect adjustments using partial network data through the lens of structural causal models. We also illustrate procedures to assign treatments using only partial network data, with the goal of either minimizing estimator variance or optimally seeding. We derive single network asymptotic results applicable to a variety of choices for an underlying graph model. We validate our approach using simulated experiments on observed graphs with applications to information diffusion in India and Malawi.

Bayesian Hyperbolic Multidimensional Scaling

Multidimensional scaling (MDS) is a widely used approach to representing high-dimensional, dependent data. MDS works by assigning each observation a location on a low-dimensional geometric manifold, with distance on the manifold representing similarity. We propose a Bayesian approach to multidimensional scaling when the low-dimensional manifold is hyperbolic. Using hyperbolic space facilitates representing tree-like structure common in many settings (e.g. text or genetic data with hierarchical structure). A Bayesian approach provides regularization that minimizes the impact of uncertainty or measurement error in the observed data. We also propose a case-control likelihood approximation that allows for efficient sampling from the posterior in larger data settings, reducing computational complexity from approximately $O(n^2)$ to $O(n)$. We evaluate the proposed method against state-of-the-art alternatives using simulations, canonical reference datasets, and human gene expression data.

Spectral goodness-of-fit tests for complete and partial network data

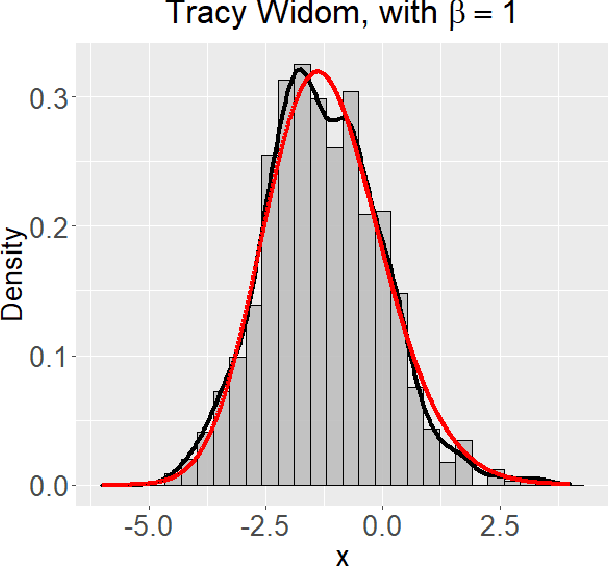
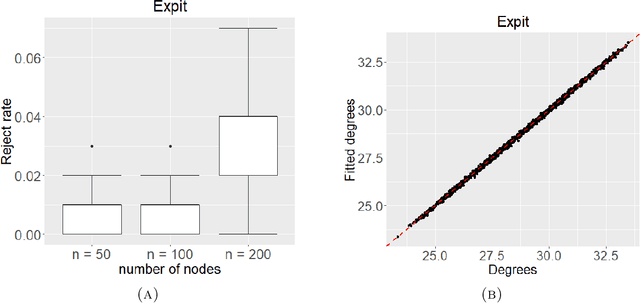
Networks describe the, often complex, relationships between individual actors. In this work, we address the question of how to determine whether a parametric model, such as a stochastic block model or latent space model, fits a dataset well and will extrapolate to similar data. We use recent results in random matrix theory to derive a general goodness-of-fit test for dyadic data. We show that our method, when applied to a specific model of interest, provides an straightforward, computationally fast way of selecting parameters in a number of commonly used network models. For example, we show how to select the dimension of the latent space in latent space models. Unlike other network goodness-of-fit methods, our general approach does not require simulating from a candidate parametric model, which can be cumbersome with large graphs, and eliminates the need to choose a particular set of statistics on the graph for comparison. It also allows us to perform goodness-of-fit tests on partial network data, such as Aggregated Relational Data. We show with simulations that our method performs well in many situations of interest. We analyze several empirically relevant networks and show that our method leads to improved community detection algorithms. R code to implement our method is available on Github.

Identifying the latent space geometry of network models through analysis of curvature

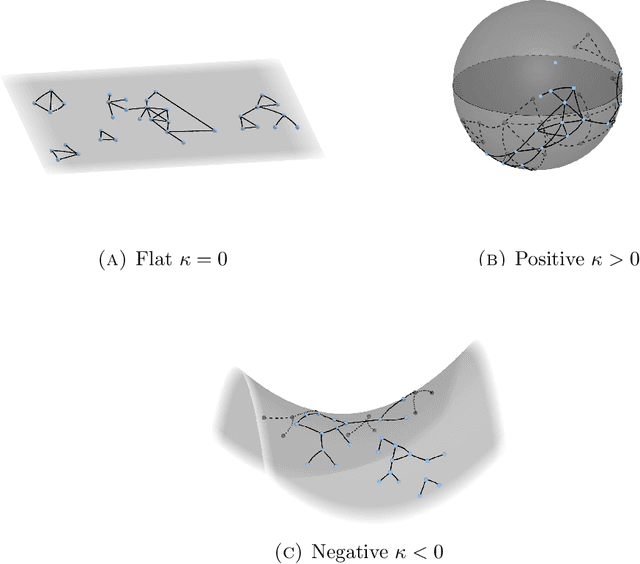
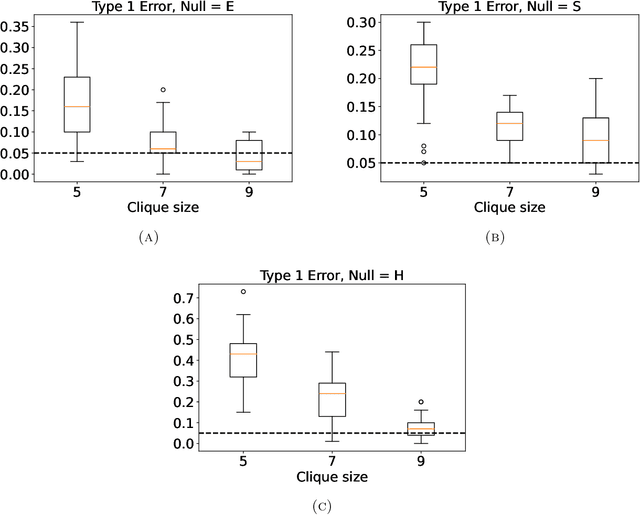
Statistically modeling networks, across numerous disciplines and contexts, is fundamentally challenging because of (often high-order) dependence between connections. A common approach assigns each person in the graph to a position on a low-dimensional manifold. Distance between individuals in this (latent) space is inversely proportional to the likelihood of forming a connection. The choice of the latent geometry (the manifold class, dimension, and curvature) has consequential impacts on the substantive conclusions of the model. More positive curvature in the manifold, for example, encourages more and tighter communities; negative curvature induces repulsion among nodes. Currently, however, the choice of the latent geometry is an a priori modeling assumption and there is limited guidance about how to make these choices in a data-driven way. In this work, we present a method to consistently estimate the manifold type, dimension, and curvature from an empirically relevant class of latent spaces: simply connected, complete Riemannian manifolds of constant curvature. Our core insight comes by representing the graph as a noisy distance matrix based on the ties between cliques. Leveraging results from statistical geometry, we develop hypothesis tests to determine whether the observed distances could plausibly be embedded isometrically in each of the candidate geometries. We explore the accuracy of our approach with simulations and then apply our approach to data-sets from economics and sociology as well as neuroscience.