Joshua Neil
A Large-Scale Database for Graph Representation Learning
Nov 16, 2020
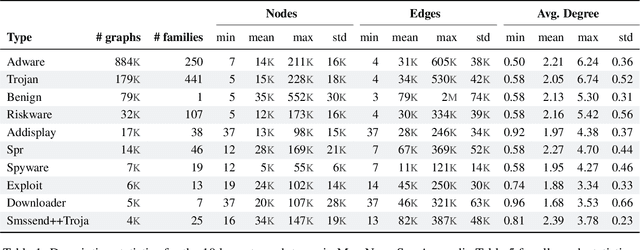
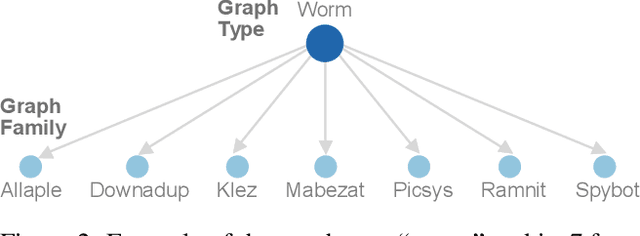

Abstract:With the rapid emergence of graph representation learning, the construction of new large-scale datasets are necessary to distinguish model capabilities and accurately assess the strengths and weaknesses of each technique. By carefully analyzing existing graph databases, we identify 3 critical components important for advancing the field of graph representation learning: (1) large graphs, (2) many graphs, and (3) class diversity. To date, no single graph database offers all of these desired properties. We introduce MalNet, the largest public graph database ever constructed, representing a large-scale ontology of software function call graphs. MalNet contains over 1.2 million graphs, averaging over 17k nodes and 39k edges per graph, across a hierarchy of 47 types and 696 families. Compared to the popular REDDIT-12K database, MalNet offers 105x more graphs, 44x larger graphs on average, and 63x the classes. We provide a detailed analysis of MalNet, discussing its properties and provenance. The unprecedented scale and diversity of MalNet offers exciting opportunities to advance the frontiers of graph representation learning---enabling new discoveries and research into imbalanced classification, explainability and the impact of class hardness. The database is publically available at www.mal-net.org.
Anomaly Detection in Large Scale Networks with Latent Space Models
Nov 13, 2019
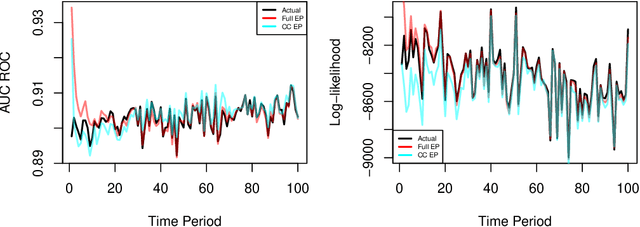
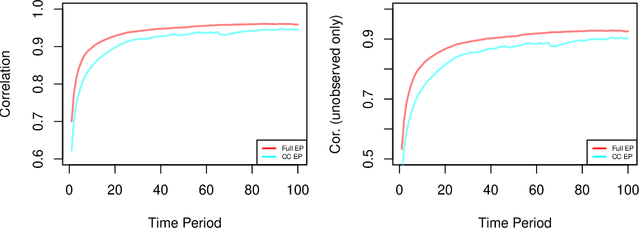
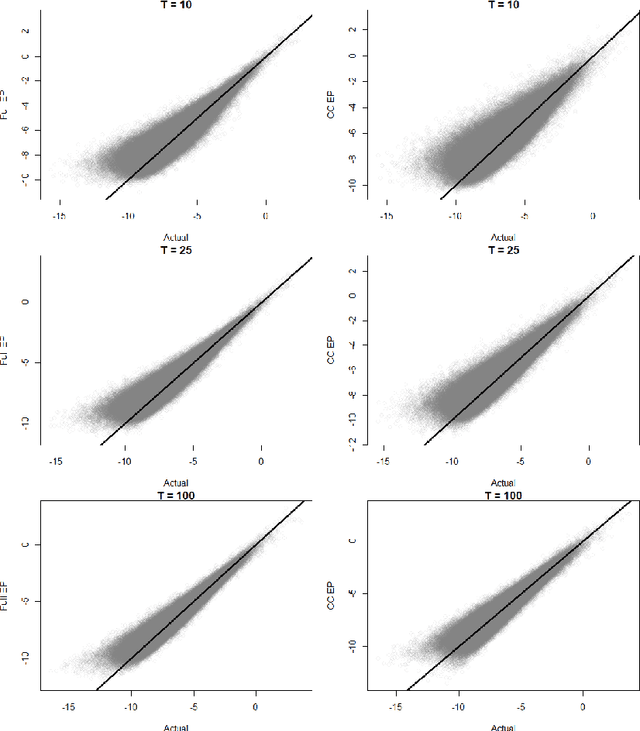
Abstract:We develop a real-time anomaly detection algorithm for directed activity on large, sparse networks. We model the propensity for future activity using a dynamic logistic model with interaction terms for sender- and receiver-specific latent factors in addition to sender- and receiver-specific popularity scores; deviations from this underlying model constitute potential anomalies. Latent nodal attributes are estimated via a variational Bayesian approach and may change over time, representing natural shifts in network activity. Estimation is augmented with a case-control approximation to take advantage of the sparsity of the network and reduces computational complexity from $O(N^2)$ to $O(E)$, where $N$ is the number of nodes and $E$ is the number of observed edges. We run our algorithm on network event records collected from an enterprise network of over 25,000 computers and are able to identify a red team attack with half the detection rate required of the model without latent interaction terms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge