Solving QMLTP Problems by Translation to Higher-order Logic

This paper describes an evaluation of Automated Theorem Proving (ATP) systems on problems taken from the QMLTP library of first-order modal logic problems. Principally, the problems are translated to higher-order logic in the TPTP languages using an embedding approach, and solved using higher-order logic ATP systems. Additionally, the results from native modal logic ATP systems are considered, and compared with those from the embedding approach. The conclusions are that (i) The embedding process is reliable and successful. (ii) The choice of backend ATP system can significantly impact the performance of the embedding approach. (iii) Native modal logic ATP systems outperform the embedding approach. (iv) The embedding approach can cope with a wider range modal logics than the native modal systems considered.

Knowledge Augmented Machine Learning with Applications in Autonomous Driving: A Survey

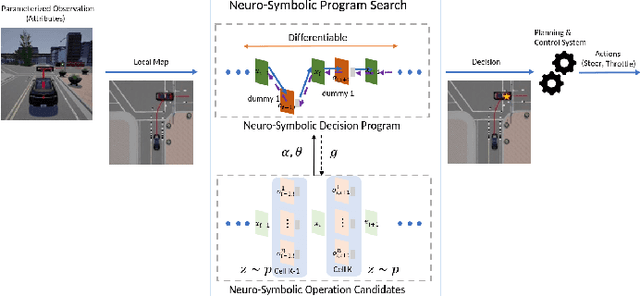
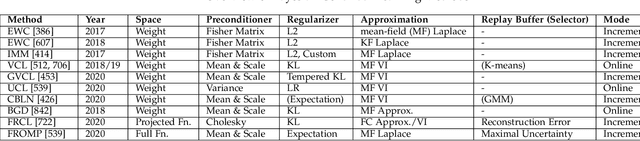
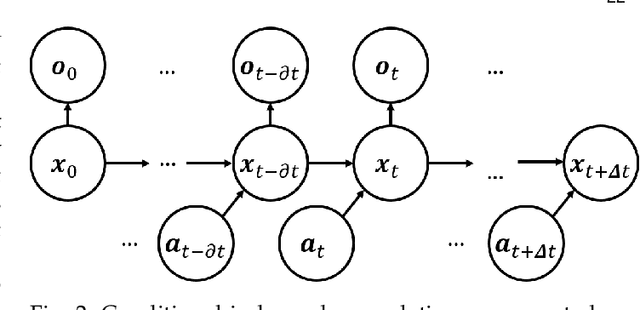
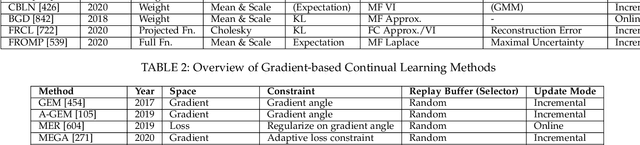
The existence of representative datasets is a prerequisite of many successful artificial intelligence and machine learning models. However, the subsequent application of these models often involves scenarios that are inadequately represented in the data used for training. The reasons for this are manifold and range from time and cost constraints to ethical considerations. As a consequence, the reliable use of these models, especially in safety-critical applications, is a huge challenge. Leveraging additional, already existing sources of knowledge is key to overcome the limitations of purely data-driven approaches, and eventually to increase the generalization capability of these models. Furthermore, predictions that conform with knowledge are crucial for making trustworthy and safe decisions even in underrepresented scenarios. This work provides an overview of existing techniques and methods in the literature that combine data-based models with existing knowledge. The identified approaches are structured according to the categories integration, extraction and conformity. Special attention is given to applications in the field of autonomous driving.

Automated Reasoning in Non-classical Logics in the TPTP World

Non-classical logics are used in a wide spectrum of disciplines, including artificial intelligence, computer science, mathematics, and philosophy. The de-facto standard infrastructure for automated theorem proving, the TPTP World, currently supports only classical logics. Similar standards for non-classical logic reasoning do not exist (yet). This hampers practical development of reasoning systems, and limits their interoperability and application. This paper describes the latest extension of the TPTP World, which provides languages and infrastructure for reasoning in non-classical logics. The extensions integrate seamlessly with the existing TPTP World.