Solving QMLTP Problems by Translation to Higher-order Logic

This paper describes an evaluation of Automated Theorem Proving (ATP) systems on problems taken from the QMLTP library of first-order modal logic problems. Principally, the problems are translated to higher-order logic in the TPTP languages using an embedding approach, and solved using higher-order logic ATP systems. Additionally, the results from native modal logic ATP systems are considered, and compared with those from the embedding approach. The conclusions are that (i) The embedding process is reliable and successful. (ii) The choice of backend ATP system can significantly impact the performance of the embedding approach. (iii) Native modal logic ATP systems outperform the embedding approach. (iv) The embedding approach can cope with a wider range modal logics than the native modal systems considered.

Who Finds the Short Proof? An Exploration of Variants of Boolos' Curious Inference using Higher-order Automated Theorem Provers

This paper reports on an exploration of variants of Boolos' curious inference, using higher-order automated theorem provers (ATPs). Surprisingly, only a single shorthand notation had to be provided by hand. All higher-order lemmas required for obtaining short proof are automatically discovered by the ATPs. Given the observations and suggestions in this paper, full proof automation of Boolos' example on the speedup of proof lengths, and related examples, now seems to be within reach for higher-order ATPs.

Automated Reasoning in Non-classical Logics in the TPTP World

Non-classical logics are used in a wide spectrum of disciplines, including artificial intelligence, computer science, mathematics, and philosophy. The de-facto standard infrastructure for automated theorem proving, the TPTP World, currently supports only classical logics. Similar standards for non-classical logic reasoning do not exist (yet). This hampers practical development of reasoning systems, and limits their interoperability and application. This paper describes the latest extension of the TPTP World, which provides languages and infrastructure for reasoning in non-classical logics. The extensions integrate seamlessly with the existing TPTP World.

Modeling in OWL 2 without Restrictions

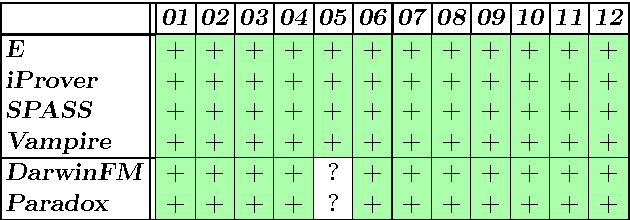
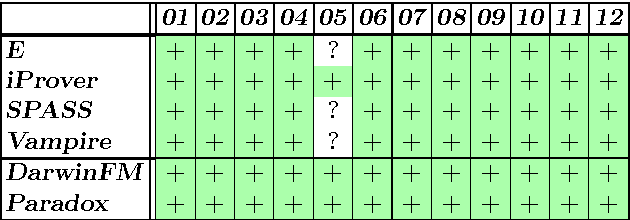
The Semantic Web ontology language OWL 2 DL comes with a variety of language features that enable sophisticated and practically useful modeling. However, the use of these features has been severely restricted in order to retain decidability of the language. For example, OWL 2 DL does not allow a property to be both transitive and asymmetric, which would be desirable, e.g., for representing an ancestor relation. In this paper, we argue that the so-called global restrictions of OWL 2 DL preclude many useful forms of modeling, by providing a catalog of basic modeling patterns that would be available in OWL 2 DL if the global restrictions were discarded. We then report on the results of evaluating several state-of-the-art OWL 2 DL reasoners on problems that use combinations of features in a way that the global restrictions are violated. The systems turn out to rely heavily on the global restrictions and are thus largely incapable of coping with the modeling patterns. Next we show how off-the-shelf first-order logic theorem proving technology can be used to perform reasoning in the OWL 2 direct semantics, the semantics that underlies OWL 2 DL, but without requiring the global restrictions. Applying a naive proof-of-concept implementation of this approach to the test problems was successful in all cases. Based on our observations, we make suggestions for future lines of research on expressive description logic-style OWL reasoning.

ATP and Presentation Service for Mizar Formalizations

This paper describes the Automated Reasoning for Mizar (MizAR) service, which integrates several automated reasoning, artificial intelligence, and presentation tools with Mizar and its authoring environment. The service provides ATP assistance to Mizar authors in finding and explaining proofs, and offers generation of Mizar problems as challenges to ATP systems. The service is based on a sound translation from the Mizar language to that of first-order ATP systems, and relies on the recent progress in application of ATP systems in large theories containing tens of thousands of available facts. We present the main features of MizAR services, followed by an account of initial experiments in finding proofs with the ATP assistance. Our initial experience indicates that the tool offers substantial help in exploring the Mizar library and in preparing new Mizar articles.

Reasoning in the OWL 2 Full Ontology Language using First-Order Automated Theorem Proving

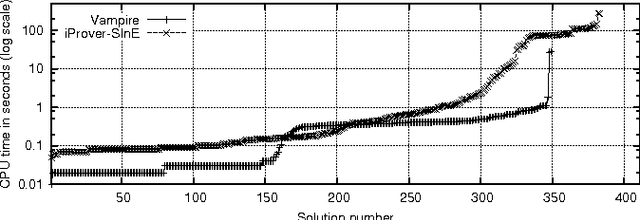
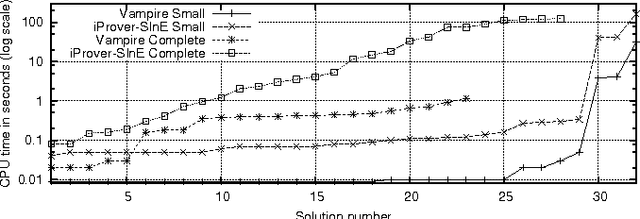
OWL 2 has been standardized by the World Wide Web Consortium (W3C) as a family of ontology languages for the Semantic Web. The most expressive of these languages is OWL 2 Full, but to date no reasoner has been implemented for this language. Consistency and entailment checking are known to be undecidable for OWL 2 Full. We have translated a large fragment of the OWL 2 Full semantics into first-order logic, and used automated theorem proving systems to do reasoning based on this theory. The results are promising, and indicate that this approach can be applied in practice for effective OWL reasoning, beyond the capabilities of current Semantic Web reasoners. This is an extended version of a paper with the same title that has been published at CADE 2011, LNAI 6803, pp. 446-460. The extended version provides appendices with additional resources that were used in the reported evaluation.

Automated Reasoning and Presentation Support for Formalizing Mathematics in Mizar

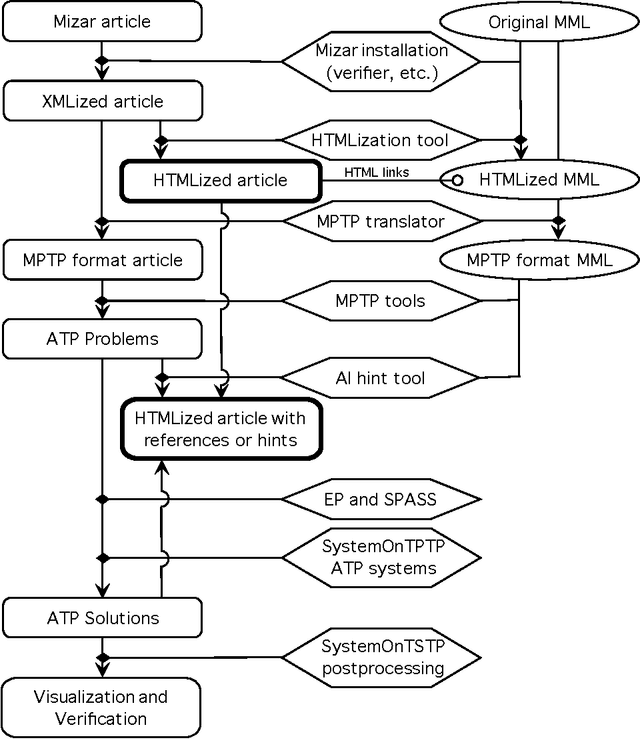
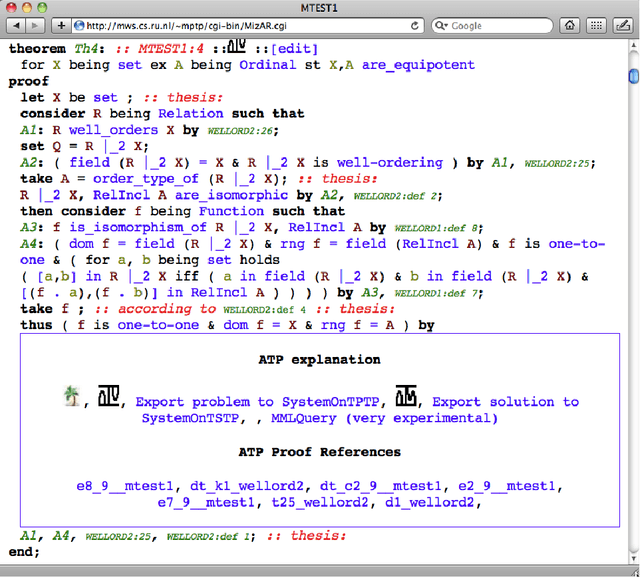
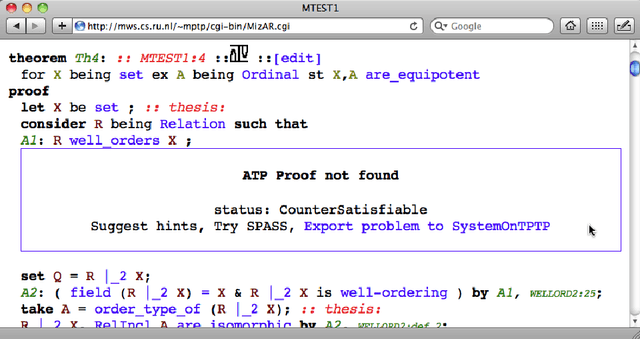
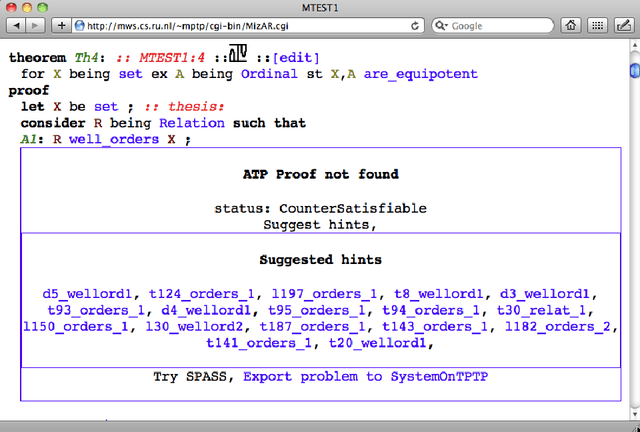
This paper presents a combination of several automated reasoning and proof presentation tools with the Mizar system for formalization of mathematics. The combination forms an online service called MizAR, similar to the SystemOnTPTP service for first-order automated reasoning. The main differences to SystemOnTPTP are the use of the Mizar language that is oriented towards human mathematicians (rather than the pure first-order logic used in SystemOnTPTP), and setting the service in the context of the large Mizar Mathematical Library of previous theorems,definitions, and proofs (rather than the isolated problems that are solved in SystemOnTPTP). These differences poses new challenges and new opportunities for automated reasoning and for proof presentation tools. This paper describes the overall structure of MizAR, and presents the automated reasoning systems and proof presentation tools that are combined to make MizAR a useful mathematical service.