Unobserved classes and extra variables in high-dimensional discriminant analysis

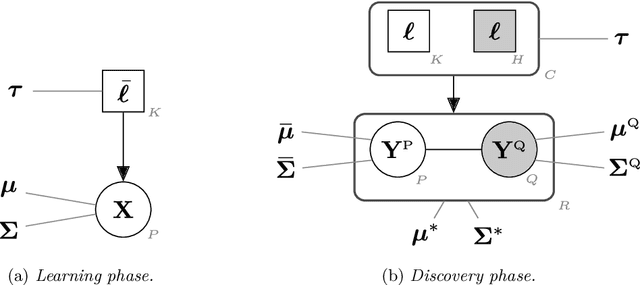
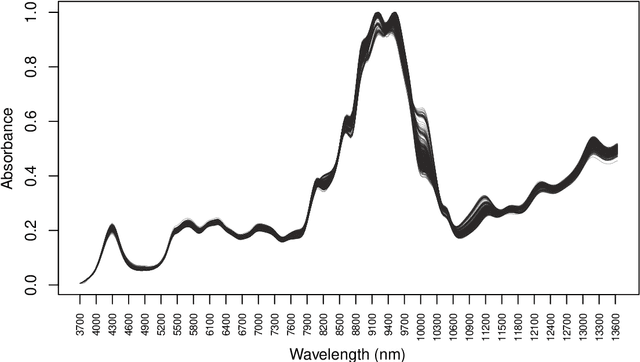
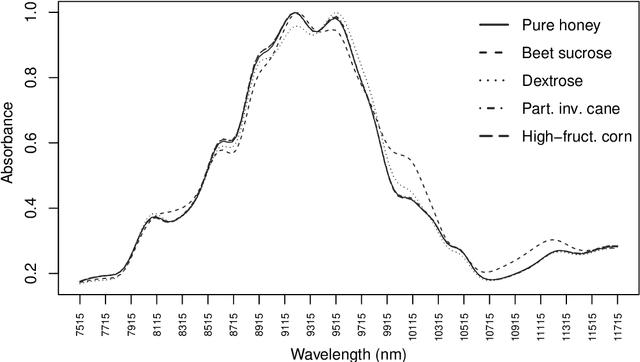
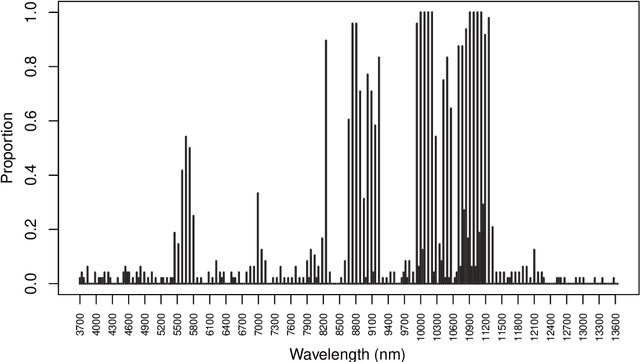
In supervised classification problems, the test set may contain data points belonging to classes not observed in the learning phase. Moreover, the same units in the test data may be measured on a set of additional variables recorded at a subsequent stage with respect to when the learning sample was collected. In this situation, the classifier built in the learning phase needs to adapt to handle potential unknown classes and the extra dimensions. We introduce a model-based discriminant approach, Dimension-Adaptive Mixture Discriminant Analysis (D-AMDA), which can detect unobserved classes and adapt to the increasing dimensionality. Model estimation is carried out via a full inductive approach based on an EM algorithm. The method is then embedded in a more general framework for adaptive variable selection and classification suitable for data of large dimensions. A simulation study and an artificial experiment related to classification of adulterated honey samples are used to validate the ability of the proposed framework to deal with complex situations.

Handling missing data in model-based clustering

Gaussian Mixture models (GMMs) are a powerful tool for clustering, classification and density estimation when clustering structures are embedded in the data. The presence of missing values can largely impact the GMMs estimation process, thus handling missing data turns out to be a crucial point in clustering, classification and density estimation. Several techniques have been developed to impute the missing values before model estimation. Among these, multiple imputation is a simple and useful general approach to handle missing data. In this paper we propose two different methods to fit Gaussian mixtures in the presence of missing data. Both methods use a variant of the Monte Carlo Expectation-Maximisation (MCEM) algorithm for data augmentation. Thus, multiple imputations are performed during the E-step, followed by the standard M-step for a given eigen-decomposed component-covariance matrix. We show that the proposed methods outperform the multiple imputation approach, both in terms of clusters identification and density estimation.

Variable Selection Methods for Model-based Clustering

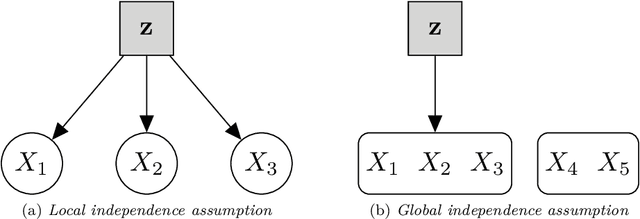
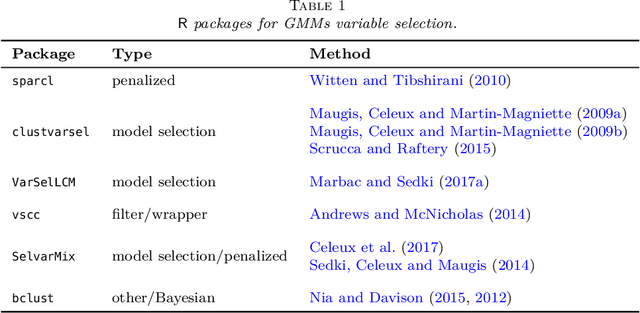
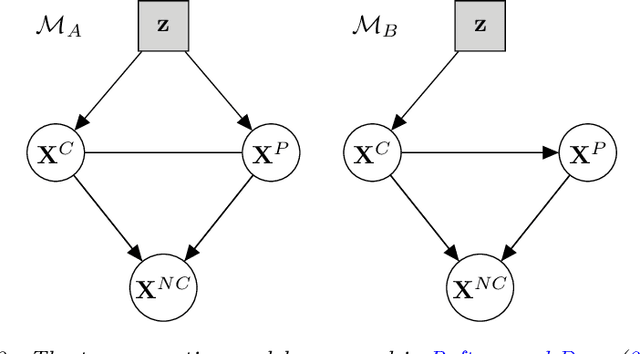
Model-based clustering is a popular approach for clustering multivariate data which has seen applications in numerous fields. Nowadays, high-dimensional data are more and more common and the model-based clustering approach has adapted to deal with the increasing dimensionality. In particular, the development of variable selection techniques has received a lot of attention and research effort in recent years. Even for small size problems, variable selection has been advocated to facilitate the interpretation of the clustering results. This review provides a summary of the methods developed for variable selection in model-based clustering. Existing R packages implementing the different methods are indicated and illustrated in application to two data analysis examples.

Bayesian nonparametric Plackett-Luce models for the analysis of preferences for college degree programmes

In this paper we propose a Bayesian nonparametric model for clustering partial ranking data. We start by developing a Bayesian nonparametric extension of the popular Plackett-Luce choice model that can handle an infinite number of choice items. Our framework is based on the theory of random atomic measures, with the prior specified by a completely random measure. We characterise the posterior distribution given data, and derive a simple and effective Gibbs sampler for posterior simulation. We then develop a Dirichlet process mixture extension of our model and apply it to investigate the clustering of preferences for college degree programmes amongst Irish secondary school graduates. The existence of clusters of applicants who have similar preferences for degree programmes is established and we determine that subject matter and geographical location of the third level institution characterise these clusters.