Flatness-aware Sequential Learning Generates Resilient Backdoors

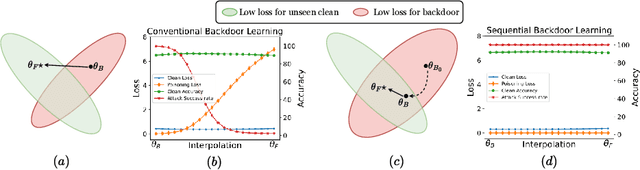
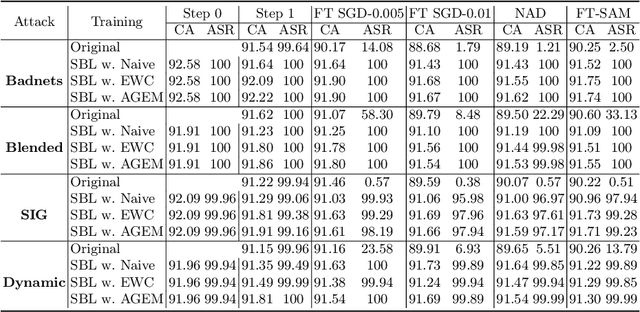
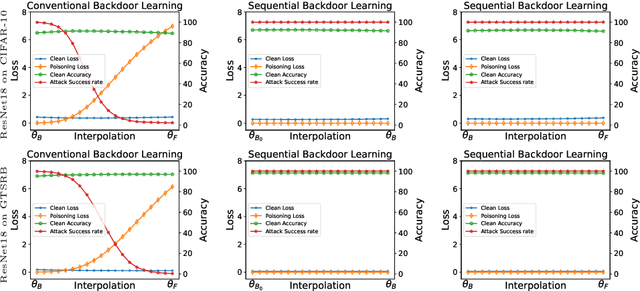
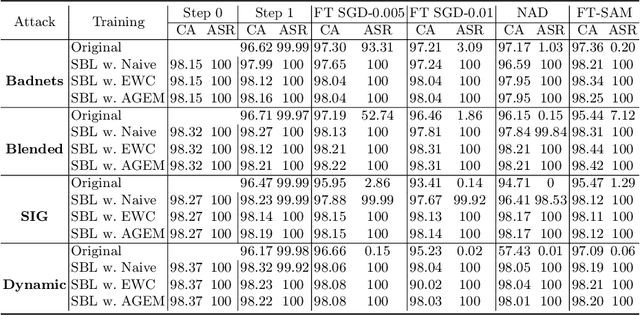
Recently, backdoor attacks have become an emerging threat to the security of machine learning models. From the adversary's perspective, the implanted backdoors should be resistant to defensive algorithms, but some recently proposed fine-tuning defenses can remove these backdoors with notable efficacy. This is mainly due to the catastrophic forgetting (CF) property of deep neural networks. This paper counters CF of backdoors by leveraging continual learning (CL) techniques. We begin by investigating the connectivity between a backdoored and fine-tuned model in the loss landscape. Our analysis confirms that fine-tuning defenses, especially the more advanced ones, can easily push a poisoned model out of the backdoor regions, making it forget all about the backdoors. Based on this finding, we re-formulate backdoor training through the lens of CL and propose a novel framework, named Sequential Backdoor Learning (SBL), that can generate resilient backdoors. This framework separates the backdoor poisoning process into two tasks: the first task learns a backdoored model, while the second task, based on the CL principles, moves it to a backdoored region resistant to fine-tuning. We additionally propose to seek flatter backdoor regions via a sharpness-aware minimizer in the framework, further strengthening the durability of the implanted backdoor. Finally, we demonstrate the effectiveness of our method through extensive empirical experiments on several benchmark datasets in the backdoor domain. The source code is available at https://github.com/mail-research/SBL-resilient-backdoors

Wicked Oddities: Selectively Poisoning for Effective Clean-Label Backdoor Attacks

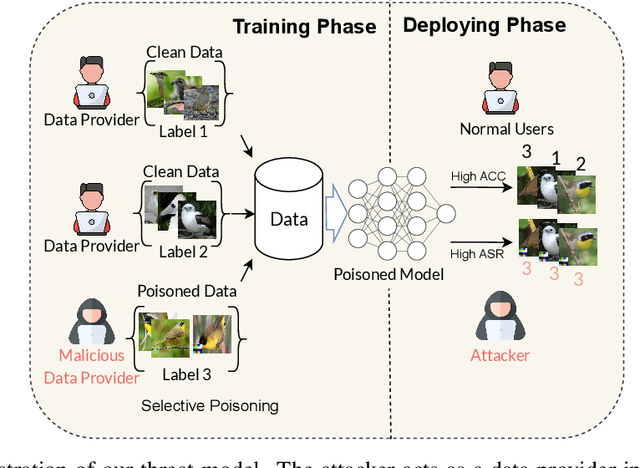
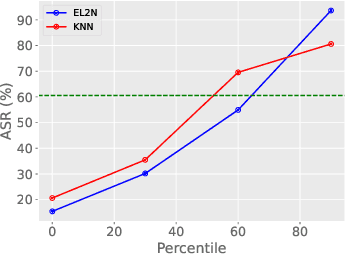
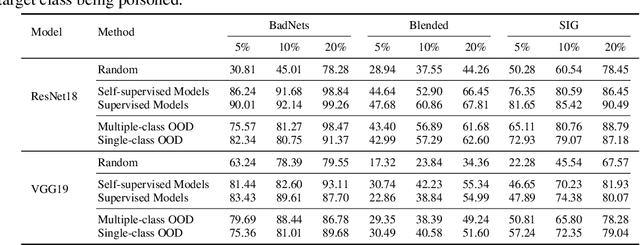
Deep neural networks are vulnerable to backdoor attacks, a type of adversarial attack that poisons the training data to manipulate the behavior of models trained on such data. Clean-label attacks are a more stealthy form of backdoor attacks that can perform the attack without changing the labels of poisoned data. Early works on clean-label attacks added triggers to a random subset of the training set, ignoring the fact that samples contribute unequally to the attack's success. This results in high poisoning rates and low attack success rates. To alleviate the problem, several supervised learning-based sample selection strategies have been proposed. However, these methods assume access to the entire labeled training set and require training, which is expensive and may not always be practical. This work studies a new and more practical (but also more challenging) threat model where the attacker only provides data for the target class (e.g., in face recognition systems) and has no knowledge of the victim model or any other classes in the training set. We study different strategies for selectively poisoning a small set of training samples in the target class to boost the attack success rate in this setting. Our threat model poses a serious threat in training machine learning models with third-party datasets, since the attack can be performed effectively with limited information. Experiments on benchmark datasets illustrate the effectiveness of our strategies in improving clean-label backdoor attacks.

Improving Heterogeneous Graph Learning with Weighted Mixed-Curvature Product Manifold

In graph representation learning, it is important that the complex geometric structure of the input graph, e.g. hidden relations among nodes, is well captured in embedding space. However, standard Euclidean embedding spaces have a limited capacity in representing graphs of varying structures. A promising candidate for the faithful embedding of data with varying structure is product manifolds of component spaces of different geometries (spherical, hyperbolic, or euclidean). In this paper, we take a closer look at the structure of product manifold embedding spaces and argue that each component space in a product contributes differently to expressing structures in the input graph, hence should be weighted accordingly. This is different from previous works which consider the roles of different components equally. We then propose WEIGHTED-PM, a data-driven method for learning embedding of heterogeneous graphs in weighted product manifolds. Our method utilizes the topological information of the input graph to automatically determine the weight of each component in product spaces. Extensive experiments on synthetic and real-world graph datasets demonstrate that WEIGHTED-PM is capable of learning better graph representations with lower geometric distortion from input data, and performs better on multiple downstream tasks, such as word similarity learning, top-$k$ recommendation, and knowledge graph embedding.

A Cosine Similarity-based Method for Out-of-Distribution Detection

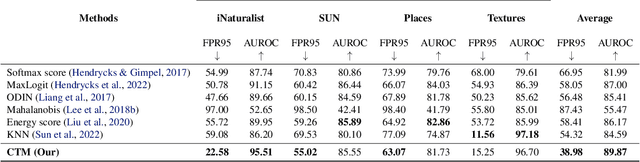
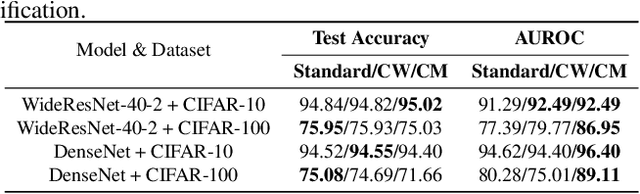
The ability to detect OOD data is a crucial aspect of practical machine learning applications. In this work, we show that cosine similarity between the test feature and the typical ID feature is a good indicator of OOD data. We propose Class Typical Matching (CTM), a post hoc OOD detection algorithm that uses a cosine similarity scoring function. Extensive experiments on multiple benchmarks show that CTM outperforms existing post hoc OOD detection methods.

Invariant Lipschitz Bandits: A Side Observation Approach

Symmetry arises in many optimization and decision-making problems, and has attracted considerable attention from the optimization community: By utilizing the existence of such symmetries, the process of searching for optimal solutions can be improved significantly. Despite its success in (offline) optimization, the utilization of symmetries has not been well examined within the online optimization settings, especially in the bandit literature. As such, in this paper we study the invariant Lipschitz bandit setting, a subclass of the Lipschitz bandits where the reward function and the set of arms are preserved under a group of transformations. We introduce an algorithm named \texttt{UniformMesh-N}, which naturally integrates side observations using group orbits into the \texttt{UniformMesh} algorithm (\cite{Kleinberg2005_UniformMesh}), which uniformly discretizes the set of arms. Using the side-observation approach, we prove an improved regret upper bound, which depends on the cardinality of the group, given that the group is finite. We also prove a matching regret's lower bound for the invariant Lipschitz bandit class (up to logarithmic factors). We hope that our work will ignite further investigation of symmetry in bandit theory and sequential decision-making theory in general.