Estimating Model Performance on External Samples from Their Limited Statistical Characteristics

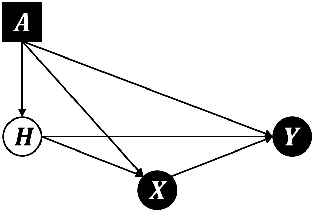
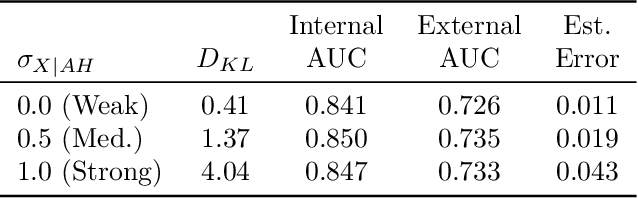
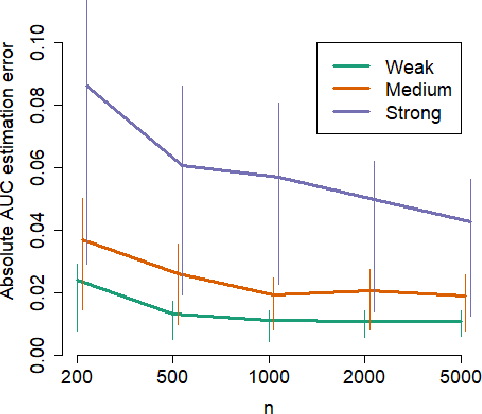
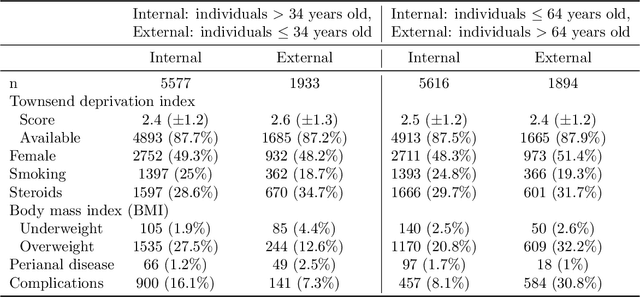
Methods that address data shifts usually assume full access to multiple datasets. In the healthcare domain, however, privacy-preserving regulations as well as commercial interests limit data availability and, as a result, researchers can typically study only a small number of datasets. In contrast, limited statistical characteristics of specific patient samples are much easier to share and may be available from previously published literature or focused collaborative efforts. Here, we propose a method that estimates model performance in external samples from their limited statistical characteristics. We search for weights that induce internal statistics that are similar to the external ones; and that are closest to uniform. We then use model performance on the weighted internal sample as an estimation for the external counterpart. We evaluate the proposed algorithm on simulated data as well as electronic medical record data for two risk models, predicting complications in ulcerative colitis patients and stroke in women diagnosed with atrial fibrillation. In the vast majority of cases, the estimated external performance is much closer to the actual one than the internal performance. Our proposed method may be an important building block in training robust models and detecting potential model failures in external environments.

Adversarial Balancing for Causal Inference

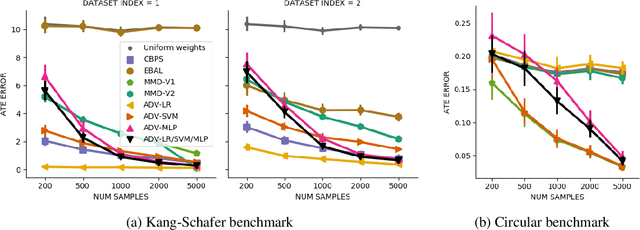
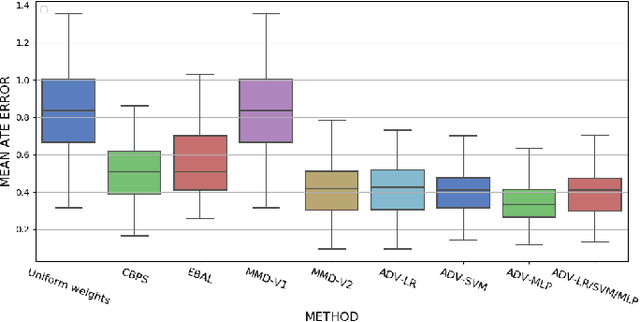
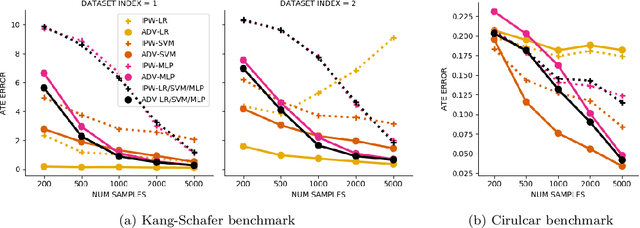
Biases in observational data pose a major challenge to estimation methods for the effect of treatments. An important technique that accounts for these biases is reweighting samples to minimize the discrepancy between treatment groups. Inverse probability weighting, a popular weighting technique, models the conditional treatment probability given covariates. However, it is overly sensitive to model misspecification and suffers from large estimation variance. Recent methods attempt to alleviate these limitations by finding weights that minimize a selected discrepancy measure between the reweighted populations. We present a new reweighting approach that uses classification error as a measure of similarity between datasets. Our proposed framework uses bi-level optimization to alternately train a discriminator to minimize classification error, and a balancing weights generator to maximize this error. This approach borrows principles from generative adversarial networks (GANs) that aim to exploit the power of classifiers for discrepancy measure estimation. We tested our approach on several benchmarks. The results of our experiments demonstrate the effectiveness and robustness of this approach in estimating causal effects under different data generating settings.

Incorporating Expressive Graphical Models in Variational Approximations: Chain-Graphs and Hidden Variables

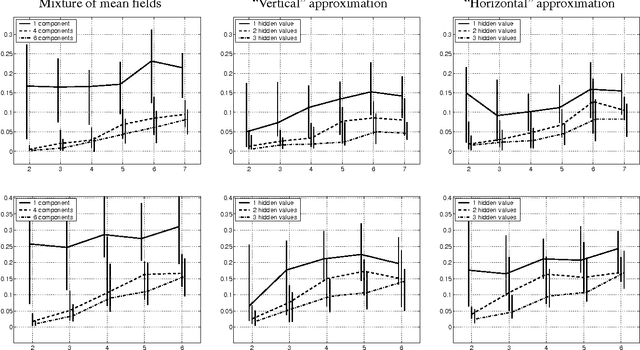
Global variational approximation methods in graphical models allow efficient approximate inference of complex posterior distributions by using a simpler model. The choice of the approximating model determines a tradeoff between the complexity of the approximation procedure and the quality of the approximation. In this paper, we consider variational approximations based on two classes of models that are richer than standard Bayesian networks, Markov networks or mixture models. As such, these classes allow to find better tradeoffs in the spectrum of approximations. The first class of models are chain graphs, which capture distributions that are partially directed. The second class of models are directed graphs (Bayesian networks) with additional latent variables. Both classes allow representation of multi-variable dependencies that cannot be easily represented within a Bayesian network.

Continuous Time Markov Networks

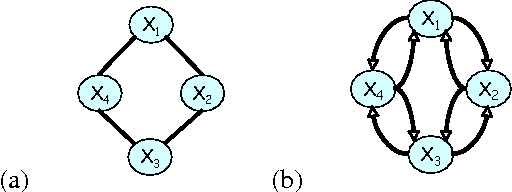
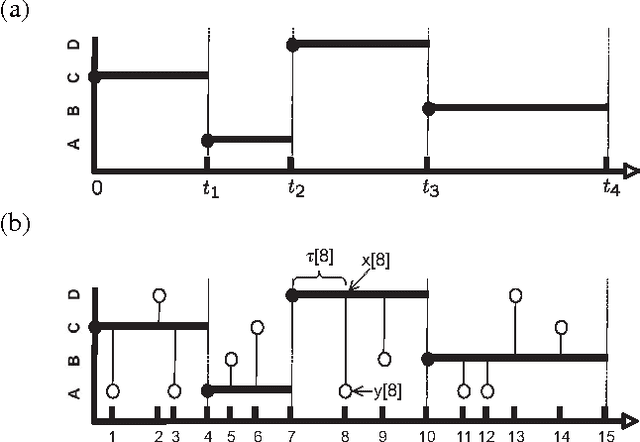
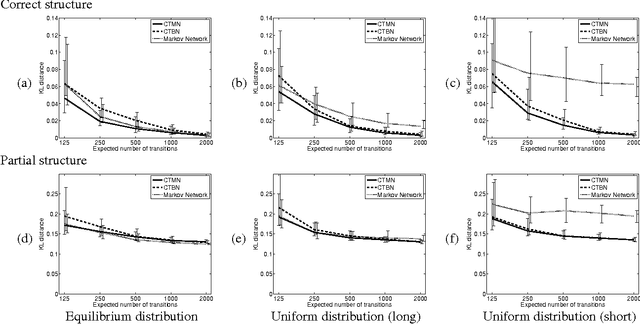
A central task in many applications is reasoning about processes that change in a continuous time. The mathematical framework of Continuous Time Markov Processes provides the basic foundations for modeling such systems. Recently, Nodelman et al introduced continuous time Bayesian networks (CTBNs), which allow a compact representation of continuous-time processes over a factored state space. In this paper, we introduce continuous time Markov networks (CTMNs), an alternative representation language that represents a different type of continuous-time dynamics. In many real life processes, such as biological and chemical systems, the dynamics of the process can be naturally described as an interplay between two forces - the tendency of each entity to change its state, and the overall fitness or energy function of the entire system. In our model, the first force is described by a continuous-time proposal process that suggests possible local changes to the state of the system at different rates. The second force is represented by a Markov network that encodes the fitness, or desirability, of different states; a proposed local change is then accepted with a probability that is a function of the change in the fitness distribution. We show that the fitness distribution is also the stationary distribution of the Markov process, so that this representation provides a characterization of a temporal process whose stationary distribution has a compact graphical representation. This allows us to naturally capture a different type of structure in complex dynamical processes, such as evolving biological sequences. We describe the semantics of the representation, its basic properties, and how it compares to CTBNs. We also provide algorithms for learning such models from data, and discuss its applicability to biological sequence evolution.

Gibbs Sampling in Factorized Continuous-Time Markov Processes

A central task in many applications is reasoning about processes that change over continuous time. Continuous-Time Bayesian Networks is a general compact representation language for multi-component continuous-time processes. However, exact inference in such processes is exponential in the number of components, and thus infeasible for most models of interest. Here we develop a novel Gibbs sampling procedure for multi-component processes. This procedure iteratively samples a trajectory for one of the components given the remaining ones. We show how to perform exact sampling that adapts to the natural time scale of the sampled process. Moreover, we show that this sampling procedure naturally exploits the structure of the network to reduce the computational cost of each step. This procedure is the first that can provide asymptotically unbiased approximation in such processes.

Mean Field Variational Approximation for Continuous-Time Bayesian Networks

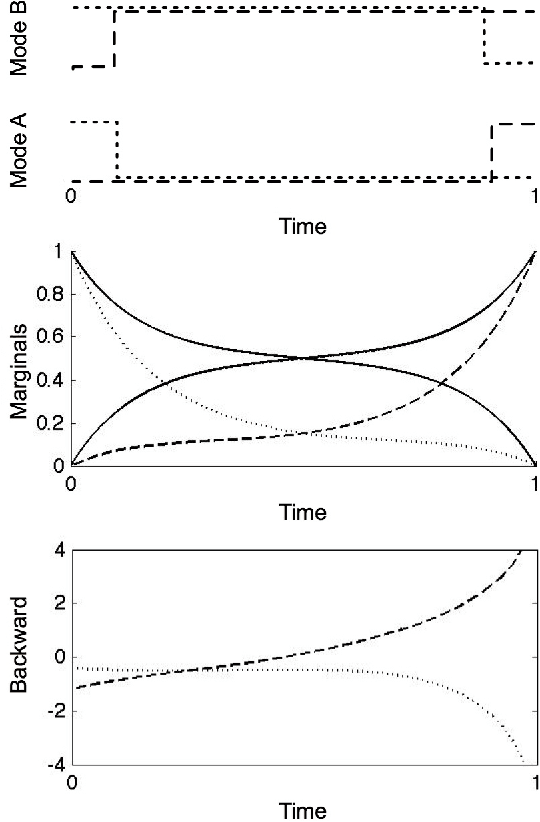
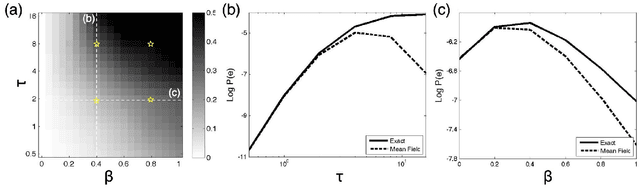
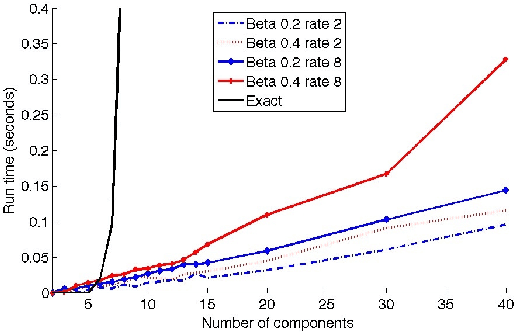
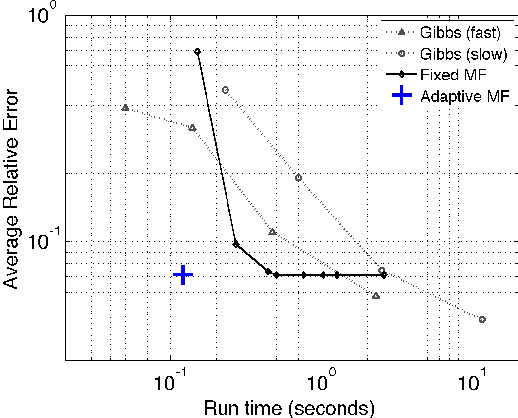
Continuous-time Bayesian networks is a natural structured representation language for multicomponent stochastic processes that evolve continuously over time. Despite the compact representation, inference in such models is intractable even in relatively simple structured networks. Here we introduce a mean field variational approximation in which we use a product of inhomogeneous Markov processes to approximate a distribution over trajectories. This variational approach leads to a globally consistent distribution, which can be efficiently queried. Additionally, it provides a lower bound on the probability of observations, thus making it attractive for learning tasks. We provide the theoretical foundations for the approximation, an efficient implementation that exploits the wide range of highly optimized ordinary differential equations (ODE) solvers, experimentally explore characterizations of processes for which this approximation is suitable, and show applications to a large-scale realworld inference problem.