Continuous Time Markov Networks

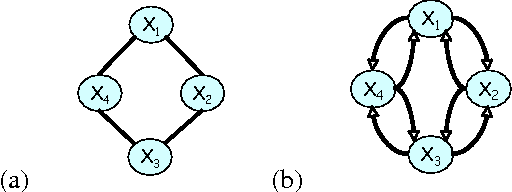
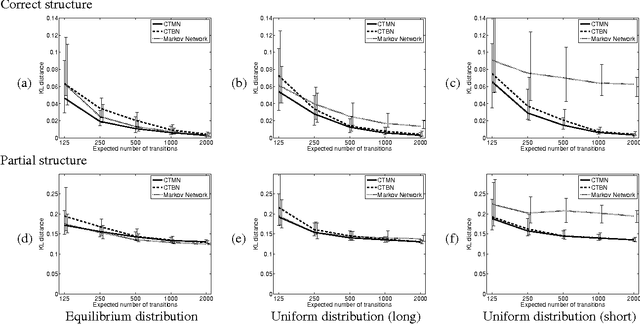
A central task in many applications is reasoning about processes that change in a continuous time. The mathematical framework of Continuous Time Markov Processes provides the basic foundations for modeling such systems. Recently, Nodelman et al introduced continuous time Bayesian networks (CTBNs), which allow a compact representation of continuous-time processes over a factored state space. In this paper, we introduce continuous time Markov networks (CTMNs), an alternative representation language that represents a different type of continuous-time dynamics. In many real life processes, such as biological and chemical systems, the dynamics of the process can be naturally described as an interplay between two forces - the tendency of each entity to change its state, and the overall fitness or energy function of the entire system. In our model, the first force is described by a continuous-time proposal process that suggests possible local changes to the state of the system at different rates. The second force is represented by a Markov network that encodes the fitness, or desirability, of different states; a proposed local change is then accepted with a probability that is a function of the change in the fitness distribution. We show that the fitness distribution is also the stationary distribution of the Markov process, so that this representation provides a characterization of a temporal process whose stationary distribution has a compact graphical representation. This allows us to naturally capture a different type of structure in complex dynamical processes, such as evolving biological sequences. We describe the semantics of the representation, its basic properties, and how it compares to CTBNs. We also provide algorithms for learning such models from data, and discuss its applicability to biological sequence evolution.

Dimension Reduction in Singularly Perturbed Continuous-Time Bayesian Networks

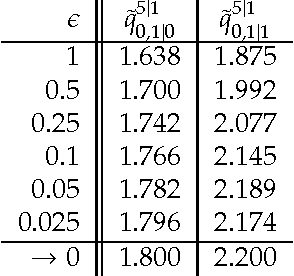
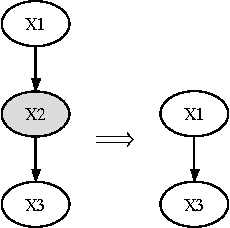
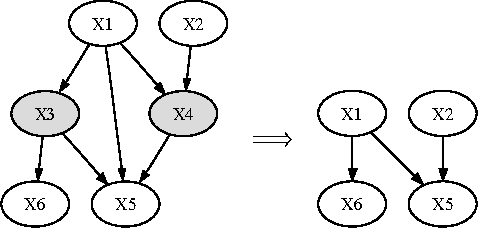
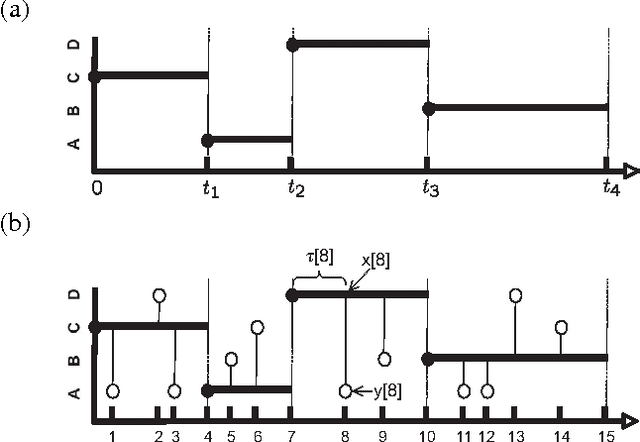
Continuous-time Bayesian networks (CTBNs) are graphical representations of multi-component continuous-time Markov processes as directed graphs. The edges in the network represent direct influences among components. The joint rate matrix of the multi-component process is specified by means of conditional rate matrices for each component separately. This paper addresses the situation where some of the components evolve on a time scale that is much shorter compared to the time scale of the other components. In this paper, we prove that in the limit where the separation of scales is infinite, the Markov process converges (in distribution, or weakly) to a reduced, or effective Markov process that only involves the slow components. We also demonstrate that for reasonable separation of scale (an order of magnitude) the reduced process is a good approximation of the marginal process over the slow components. We provide a simple procedure for building a reduced CTBN for this effective process, with conditional rate matrices that can be directly calculated from the original CTBN, and discuss the implications for approximate reasoning in large systems.

Gibbs Sampling in Factorized Continuous-Time Markov Processes

A central task in many applications is reasoning about processes that change over continuous time. Continuous-Time Bayesian Networks is a general compact representation language for multi-component continuous-time processes. However, exact inference in such processes is exponential in the number of components, and thus infeasible for most models of interest. Here we develop a novel Gibbs sampling procedure for multi-component processes. This procedure iteratively samples a trajectory for one of the components given the remaining ones. We show how to perform exact sampling that adapts to the natural time scale of the sampled process. Moreover, we show that this sampling procedure naturally exploits the structure of the network to reduce the computational cost of each step. This procedure is the first that can provide asymptotically unbiased approximation in such processes.

Mean Field Variational Approximation for Continuous-Time Bayesian Networks

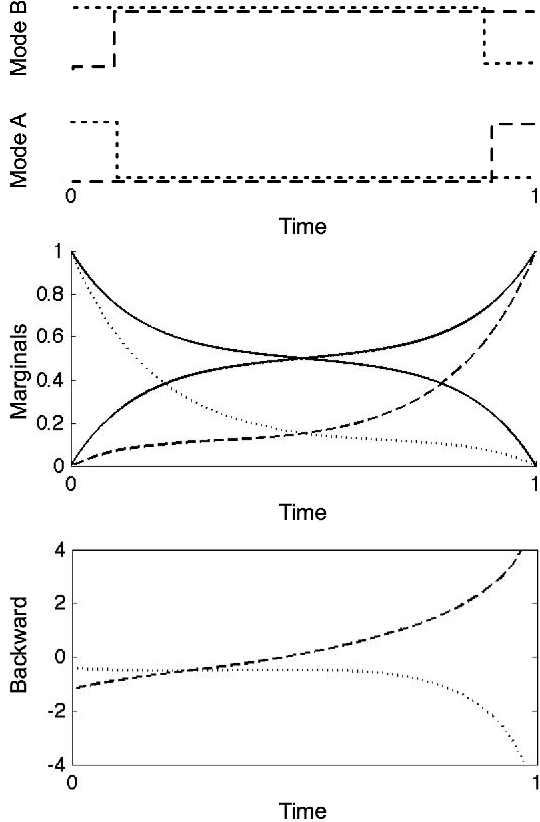
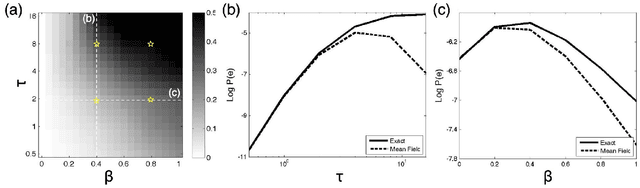
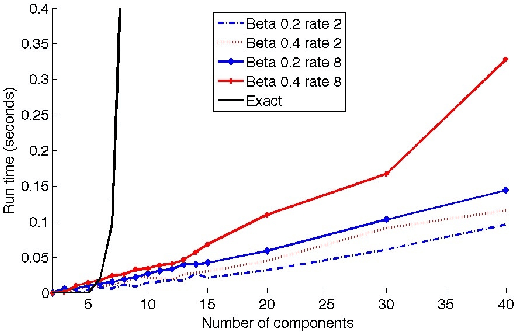
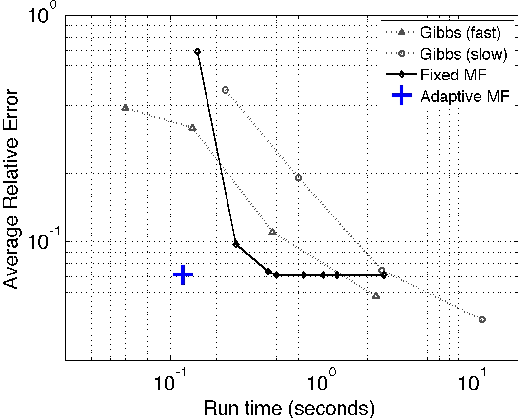
Continuous-time Bayesian networks is a natural structured representation language for multicomponent stochastic processes that evolve continuously over time. Despite the compact representation, inference in such models is intractable even in relatively simple structured networks. Here we introduce a mean field variational approximation in which we use a product of inhomogeneous Markov processes to approximate a distribution over trajectories. This variational approach leads to a globally consistent distribution, which can be efficiently queried. Additionally, it provides a lower bound on the probability of observations, thus making it attractive for learning tasks. We provide the theoretical foundations for the approximation, an efficient implementation that exploits the wide range of highly optimized ordinary differential equations (ODE) solvers, experimentally explore characterizations of processes for which this approximation is suitable, and show applications to a large-scale realworld inference problem.