Dimension Reduction in Singularly Perturbed Continuous-Time Bayesian Networks

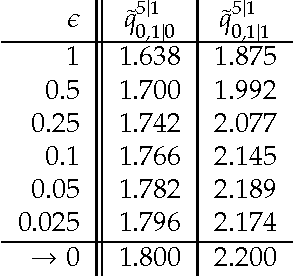
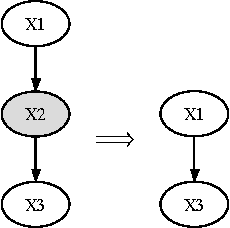
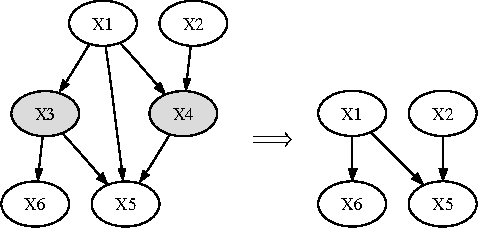
Continuous-time Bayesian networks (CTBNs) are graphical representations of multi-component continuous-time Markov processes as directed graphs. The edges in the network represent direct influences among components. The joint rate matrix of the multi-component process is specified by means of conditional rate matrices for each component separately. This paper addresses the situation where some of the components evolve on a time scale that is much shorter compared to the time scale of the other components. In this paper, we prove that in the limit where the separation of scales is infinite, the Markov process converges (in distribution, or weakly) to a reduced, or effective Markov process that only involves the slow components. We also demonstrate that for reasonable separation of scale (an order of magnitude) the reduced process is a good approximation of the marginal process over the slow components. We provide a simple procedure for building a reduced CTBN for this effective process, with conditional rate matrices that can be directly calculated from the original CTBN, and discuss the implications for approximate reasoning in large systems.