Continuous Time Markov Networks
Paper and Code
Jun 27, 2012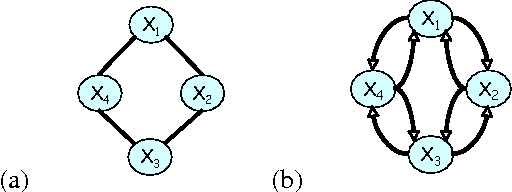
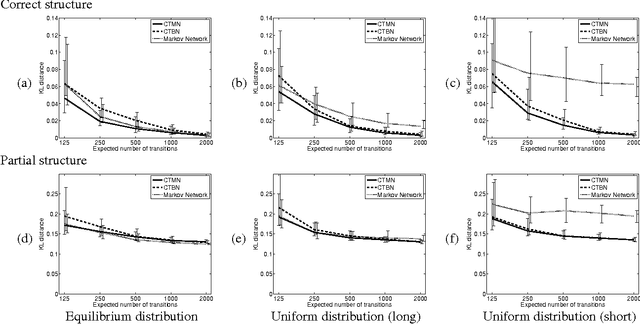
A central task in many applications is reasoning about processes that change in a continuous time. The mathematical framework of Continuous Time Markov Processes provides the basic foundations for modeling such systems. Recently, Nodelman et al introduced continuous time Bayesian networks (CTBNs), which allow a compact representation of continuous-time processes over a factored state space. In this paper, we introduce continuous time Markov networks (CTMNs), an alternative representation language that represents a different type of continuous-time dynamics. In many real life processes, such as biological and chemical systems, the dynamics of the process can be naturally described as an interplay between two forces - the tendency of each entity to change its state, and the overall fitness or energy function of the entire system. In our model, the first force is described by a continuous-time proposal process that suggests possible local changes to the state of the system at different rates. The second force is represented by a Markov network that encodes the fitness, or desirability, of different states; a proposed local change is then accepted with a probability that is a function of the change in the fitness distribution. We show that the fitness distribution is also the stationary distribution of the Markov process, so that this representation provides a characterization of a temporal process whose stationary distribution has a compact graphical representation. This allows us to naturally capture a different type of structure in complex dynamical processes, such as evolving biological sequences. We describe the semantics of the representation, its basic properties, and how it compares to CTBNs. We also provide algorithms for learning such models from data, and discuss its applicability to biological sequence evolution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge