Incorporating Expressive Graphical Models in Variational Approximations: Chain-Graphs and Hidden Variables

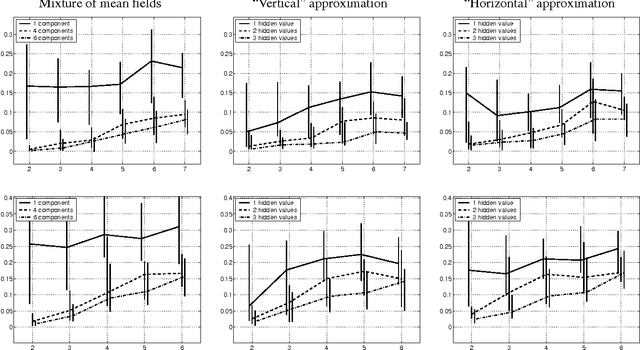
Global variational approximation methods in graphical models allow efficient approximate inference of complex posterior distributions by using a simpler model. The choice of the approximating model determines a tradeoff between the complexity of the approximation procedure and the quality of the approximation. In this paper, we consider variational approximations based on two classes of models that are richer than standard Bayesian networks, Markov networks or mixture models. As such, these classes allow to find better tradeoffs in the spectrum of approximations. The first class of models are chain graphs, which capture distributions that are partially directed. The second class of models are directed graphs (Bayesian networks) with additional latent variables. Both classes allow representation of multi-variable dependencies that cannot be easily represented within a Bayesian network.