Estimating Model Performance on External Samples from Their Limited Statistical Characteristics

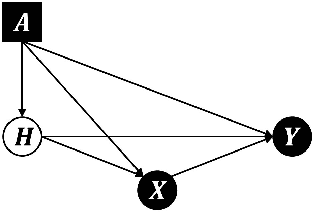
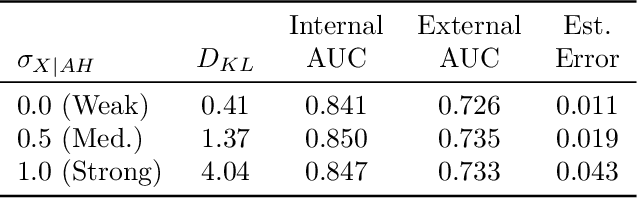
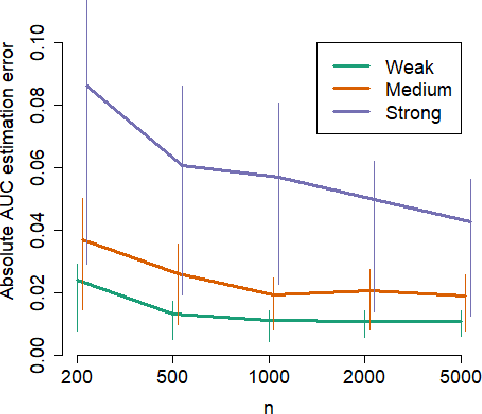
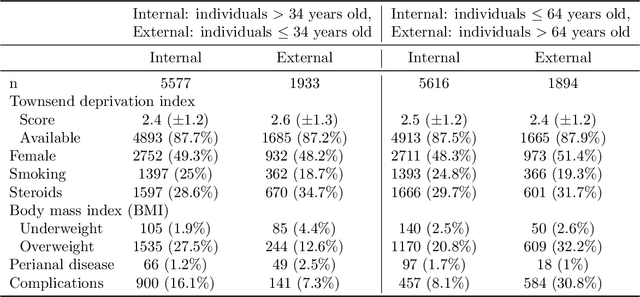
Methods that address data shifts usually assume full access to multiple datasets. In the healthcare domain, however, privacy-preserving regulations as well as commercial interests limit data availability and, as a result, researchers can typically study only a small number of datasets. In contrast, limited statistical characteristics of specific patient samples are much easier to share and may be available from previously published literature or focused collaborative efforts. Here, we propose a method that estimates model performance in external samples from their limited statistical characteristics. We search for weights that induce internal statistics that are similar to the external ones; and that are closest to uniform. We then use model performance on the weighted internal sample as an estimation for the external counterpart. We evaluate the proposed algorithm on simulated data as well as electronic medical record data for two risk models, predicting complications in ulcerative colitis patients and stroke in women diagnosed with atrial fibrillation. In the vast majority of cases, the estimated external performance is much closer to the actual one than the internal performance. Our proposed method may be an important building block in training robust models and detecting potential model failures in external environments.

Benchmarking Framework for Performance-Evaluation of Causal Inference Analysis

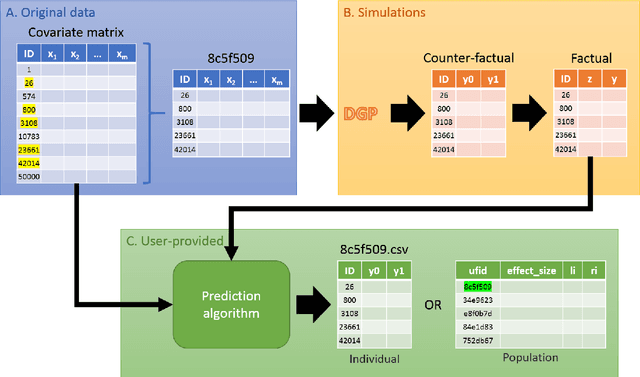
Causal inference analysis is the estimation of the effects of actions on outcomes. In the context of healthcare data this means estimating the outcome of counter-factual treatments (i.e. including treatments that were not observed) on a patient's outcome. Compared to classic machine learning methods, evaluation and validation of causal inference analysis is more challenging because ground truth data of counter-factual outcome can never be obtained in any real-world scenario. Here, we present a comprehensive framework for benchmarking algorithms that estimate causal effect. The framework includes unlabeled data for prediction, labeled data for validation, and code for automatic evaluation of algorithm predictions using both established and novel metrics. The data is based on real-world covariates, and the treatment assignments and outcomes are based on simulations, which provides the basis for validation. In this framework we address two questions: one of scaling, and the other of data-censoring. The framework is available as open source code at https://github.com/IBM-HRL-MLHLS/IBM-Causal-Inference-Benchmarking-Framework

MAP Estimation, Linear Programming and Belief Propagation with Convex Free Energies

Finding the most probable assignment (MAP) in a general graphical model is known to be NP hard but good approximations have been attained with max-product belief propagation (BP) and its variants. In particular, it is known that using BP on a single-cycle graph or tree reweighted BP on an arbitrary graph will give the MAP solution if the beliefs have no ties. In this paper we extend the setting under which BP can be used to provably extract the MAP. We define Convex BP as BP algorithms based on a convex free energy approximation and show that this class includes ordinary BP with single-cycle, tree reweighted BP and many other BP variants. We show that when there are no ties, fixed-points of convex max-product BP will provably give the MAP solution. We also show that convex sum-product BP at sufficiently small temperatures can be used to solve linear programs that arise from relaxing the MAP problem. Finally, we derive a novel condition that allows us to derive the MAP solution even if some of the convex BP beliefs have ties. In experiments, we show that our theorems allow us to find the MAP in many real-world instances of graphical models where exact inference using junction-tree is impossible.