Tractable and Provably Efficient Distributional Reinforcement Learning with General Value Function Approximation

Distributional reinforcement learning improves performance by effectively capturing environmental stochasticity, but a comprehensive theoretical understanding of its effectiveness remains elusive. In this paper, we present a regret analysis for distributional reinforcement learning with general value function approximation in a finite episodic Markov decision process setting. We first introduce a key notion of Bellman unbiasedness for a tractable and exactly learnable update via statistical functional dynamic programming. Our theoretical results show that approximating the infinite-dimensional return distribution with a finite number of moment functionals is the only method to learn the statistical information unbiasedly, including nonlinear statistical functionals. Second, we propose a provably efficient algorithm, $\texttt{SF-LSVI}$, achieving a regret bound of $\tilde{O}(d_E H^{\frac{3}{2}}\sqrt{K})$ where $H$ is the horizon, $K$ is the number of episodes, and $d_E$ is the eluder dimension of a function class.

Spectral-Risk Safe Reinforcement Learning with Convergence Guarantees

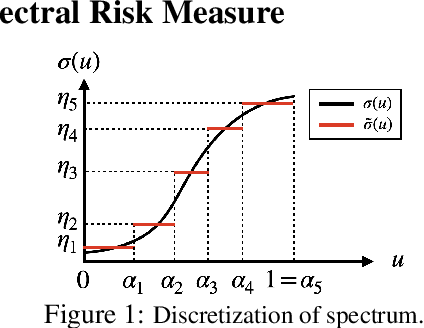
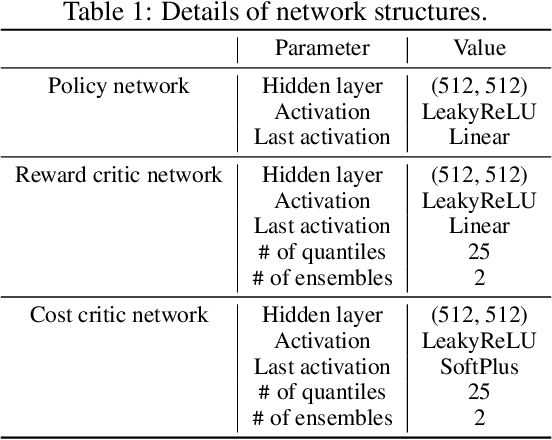
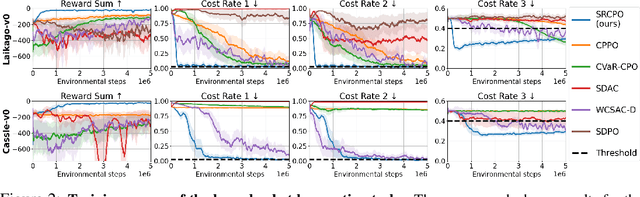
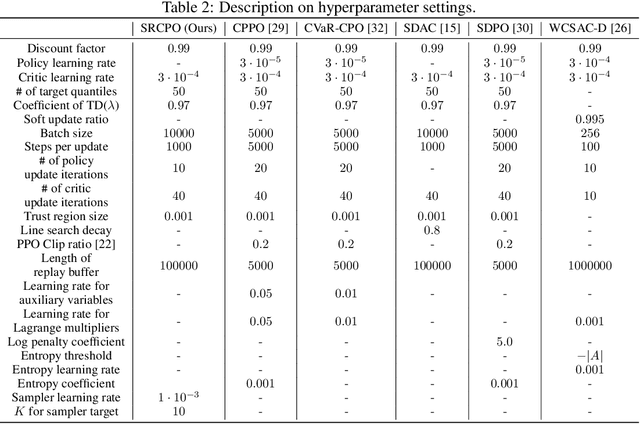
The field of risk-constrained reinforcement learning (RCRL) has been developed to effectively reduce the likelihood of worst-case scenarios by explicitly handling risk-measure-based constraints. However, the nonlinearity of risk measures makes it challenging to achieve convergence and optimality. To overcome the difficulties posed by the nonlinearity, we propose a spectral risk measure-constrained RL algorithm, spectral-risk-constrained policy optimization (SRCPO), a bilevel optimization approach that utilizes the duality of spectral risk measures. In the bilevel optimization structure, the outer problem involves optimizing dual variables derived from the risk measures, while the inner problem involves finding an optimal policy given these dual variables. The proposed method, to the best of our knowledge, is the first to guarantee convergence to an optimum in the tabular setting. Furthermore, the proposed method has been evaluated on continuous control tasks and showed the best performance among other RCRL algorithms satisfying the constraints.

On the Convergence of Continual Learning with Adaptive Methods

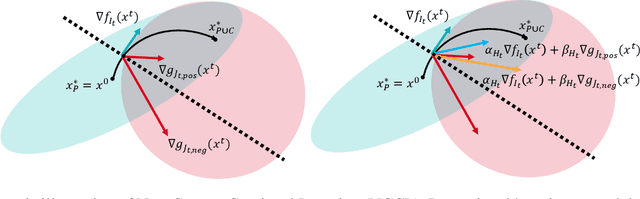
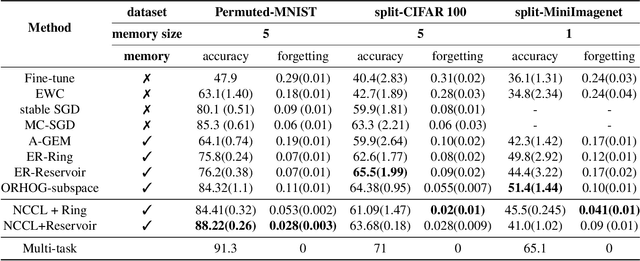
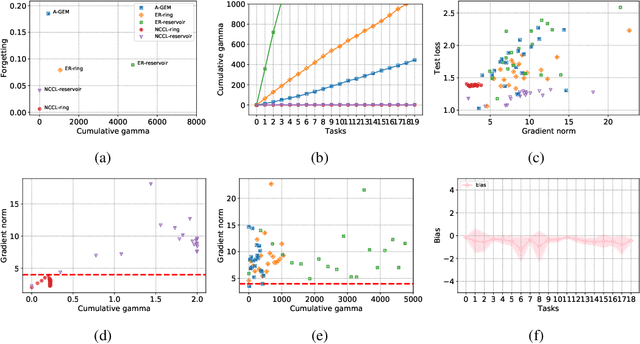
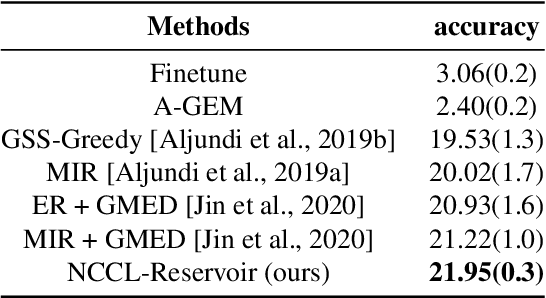
One of the objectives of continual learning is to prevent catastrophic forgetting in learning multiple tasks sequentially, and the existing solutions have been driven by the conceptualization of the plasticity-stability dilemma. However, the convergence of continual learning for each sequential task is less studied so far. In this paper, we provide a convergence analysis of memory-based continual learning with stochastic gradient descent and empirical evidence that training current tasks causes the cumulative degradation of previous tasks. We propose an adaptive method for nonconvex continual learning (NCCL), which adjusts step sizes of both previous and current tasks with the gradients. The proposed method can achieve the same convergence rate as the SGD method when the catastrophic forgetting term which we define in the paper is suppressed at each iteration. Further, we demonstrate that the proposed algorithm improves the performance of continual learning over existing methods for several image classification tasks.

SPQR: Controlling Q-ensemble Independence with Spiked Random Model for Reinforcement Learning

Alleviating overestimation bias is a critical challenge for deep reinforcement learning to achieve successful performance on more complex tasks or offline datasets containing out-of-distribution data. In order to overcome overestimation bias, ensemble methods for Q-learning have been investigated to exploit the diversity of multiple Q-functions. Since network initialization has been the predominant approach to promote diversity in Q-functions, heuristically designed diversity injection methods have been studied in the literature. However, previous studies have not attempted to approach guaranteed independence over an ensemble from a theoretical perspective. By introducing a novel regularization loss for Q-ensemble independence based on random matrix theory, we propose spiked Wishart Q-ensemble independence regularization (SPQR) for reinforcement learning. Specifically, we modify the intractable hypothesis testing criterion for the Q-ensemble independence into a tractable KL divergence between the spectral distribution of the Q-ensemble and the target Wigner's semicircle distribution. We implement SPQR in several online and offline ensemble Q-learning algorithms. In the experiments, SPQR outperforms the baseline algorithms in both online and offline RL benchmarks.

Pitfall of Optimism: Distributional Reinforcement Learning by Randomizing Risk Criterion

Distributional reinforcement learning algorithms have attempted to utilize estimated uncertainty for exploration, such as optimism in the face of uncertainty. However, using the estimated variance for optimistic exploration may cause biased data collection and hinder convergence or performance. In this paper, we present a novel distributional reinforcement learning algorithm that selects actions by randomizing risk criterion to avoid one-sided tendency on risk. We provide a perturbed distributional Bellman optimality operator by distorting the risk measure and prove the convergence and optimality of the proposed method with the weaker contraction property. Our theoretical results support that the proposed method does not fall into biased exploration and is guaranteed to converge to an optimal return. Finally, we empirically show that our method outperforms other existing distribution-based algorithms in various environments including Atari 55 games.