On the Convergence of Continual Learning with Adaptive Methods
Paper and Code
Apr 15, 2024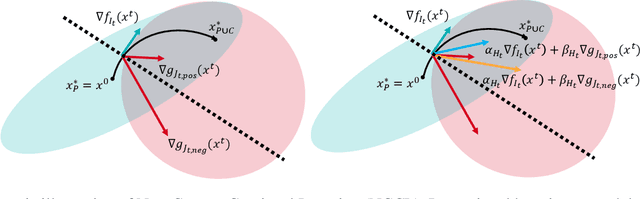
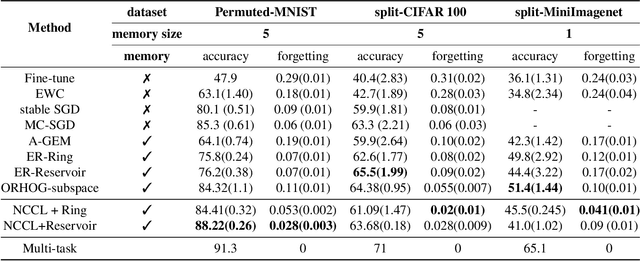
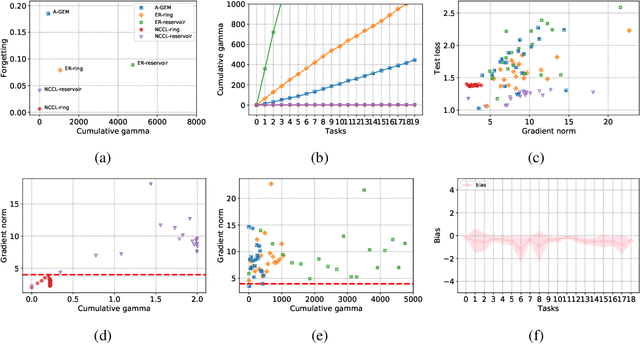
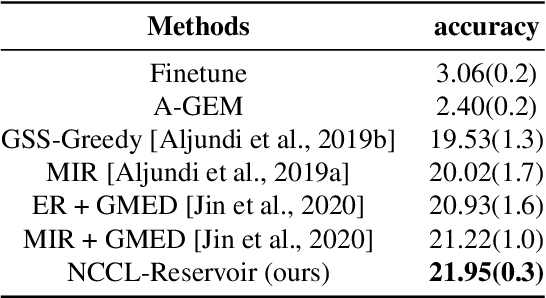
One of the objectives of continual learning is to prevent catastrophic forgetting in learning multiple tasks sequentially, and the existing solutions have been driven by the conceptualization of the plasticity-stability dilemma. However, the convergence of continual learning for each sequential task is less studied so far. In this paper, we provide a convergence analysis of memory-based continual learning with stochastic gradient descent and empirical evidence that training current tasks causes the cumulative degradation of previous tasks. We propose an adaptive method for nonconvex continual learning (NCCL), which adjusts step sizes of both previous and current tasks with the gradients. The proposed method can achieve the same convergence rate as the SGD method when the catastrophic forgetting term which we define in the paper is suppressed at each iteration. Further, we demonstrate that the proposed algorithm improves the performance of continual learning over existing methods for several image classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge