Uncertainty-aware GAN with Adaptive Loss for Robust MRI Image Enhancement

Image-to-image translation is an ill-posed problem as unique one-to-one mapping may not exist between the source and target images. Learning-based methods proposed in this context often evaluate the performance on test data that is similar to the training data, which may be impractical. This demands robust methods that can quantify uncertainty in the prediction for making informed decisions, especially for critical areas such as medical imaging. Recent works that employ conditional generative adversarial networks (GANs) have shown improved performance in learning photo-realistic image-to-image mappings between the source and the target images. However, these methods do not focus on (i)~robustness of the models to out-of-distribution (OOD)-noisy data and (ii)~uncertainty quantification. This paper proposes a GAN-based framework that (i)~models an adaptive loss function for robustness to OOD-noisy data that automatically tunes the spatially varying norm for penalizing the residuals and (ii)~estimates the per-voxel uncertainty in the predictions. We demonstrate our method on two key applications in medical imaging: (i)~undersampled magnetic resonance imaging (MRI) reconstruction (ii)~MRI modality propagation. Our experiments with two different real-world datasets show that the proposed method (i)~is robust to OOD-noisy test data and provides improved accuracy and (ii)~quantifies voxel-level uncertainty in the predictions.

Towards Lower-Dose PET using Physics-Based Uncertainty-Aware Multimodal Learning with Robustness to Out-of-Distribution Data

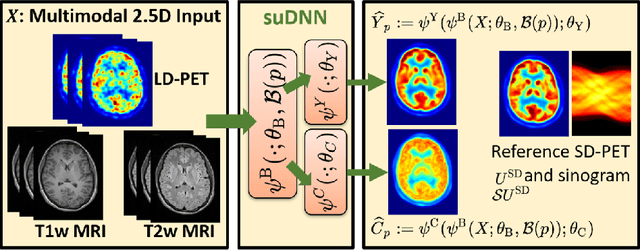
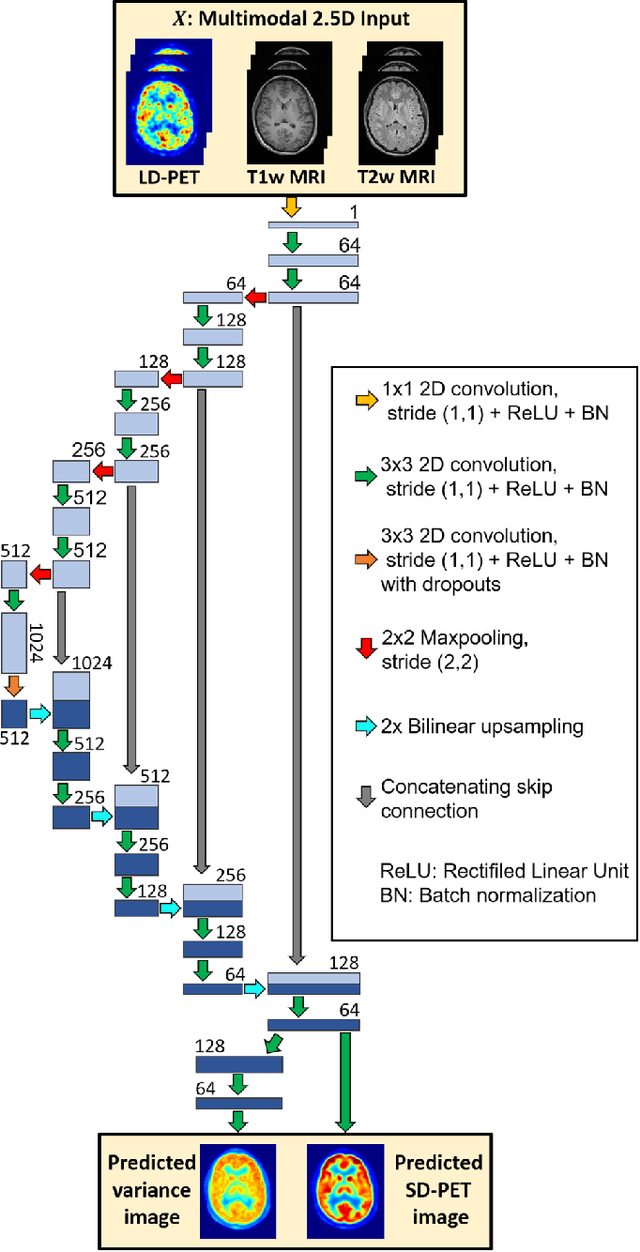
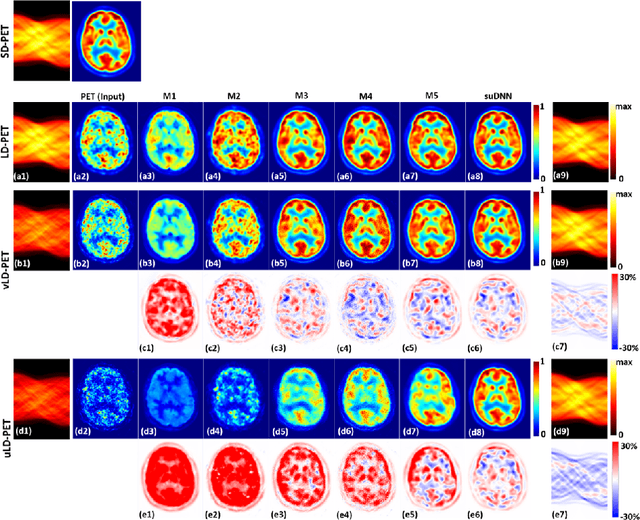
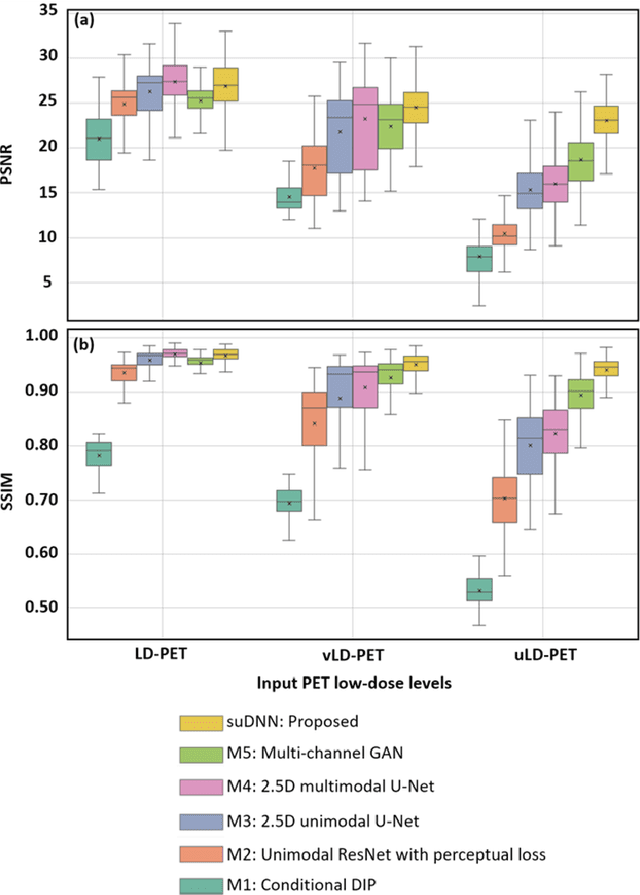
Radiation exposure in positron emission tomography (PET) imaging limits its usage in the studies of radiation-sensitive populations, e.g., pregnant women, children, and adults that require longitudinal imaging. Reducing the PET radiotracer dose or acquisition time reduces photon counts, which can deteriorate image quality. Recent deep-neural-network (DNN) based methods for image-to-image translation enable the mapping of low-quality PET images (acquired using substantially reduced dose), coupled with the associated magnetic resonance imaging (MRI) images, to high-quality PET images. However, such DNN methods focus on applications involving test data that match the statistical characteristics of the training data very closely and give little attention to evaluating the performance of these DNNs on new out-of-distribution (OOD) acquisitions. We propose a novel DNN formulation that models the (i) underlying sinogram-based physics of the PET imaging system and (ii) the uncertainty in the DNN output through the per-voxel heteroscedasticity of the residuals between the predicted and the high-quality reference images. Our sinogram-based uncertainty-aware DNN framework, namely, suDNN, estimates a standard-dose PET image using multimodal input in the form of (i) a low-dose/low-count PET image and (ii) the corresponding multi-contrast MRI images, leading to improved robustness of suDNN to OOD acquisitions. Results on in vivo simultaneous PET-MRI, and various forms of OOD data in PET-MRI, show the benefits of suDNN over the current state of the art, quantitatively and qualitatively.

Single Test Image-Based Automated Machine Learning System for Distinguishing between Trait and Diseased Blood Samples

We introduce a machine learning-based method for fully automated diagnosis of sickle cell disease of poor-quality unstained images of a mobile microscope. Our method is capable of distinguishing between diseased, trait (carrier), and normal samples unlike the previous methods that are limited to distinguishing the normal from the abnormal samples only. The novelty of this method comes from distinguishing the trait and the diseased samples from challenging images that have been captured directly in the field. The proposed approach contains two parts, the segmentation part followed by the classification part. We use a random forest algorithm to segment such challenging images acquitted through a mobile phone-based microscope. Then, we train two classifiers based on a random forest (RF) and a support vector machine (SVM) for classification. The results show superior performances of both of the classifiers not only for images which have been captured in the lab, but also for the ones which have been acquired in the field itself.

Robust Super-Resolution GAN, with Manifold-based and Perception Loss

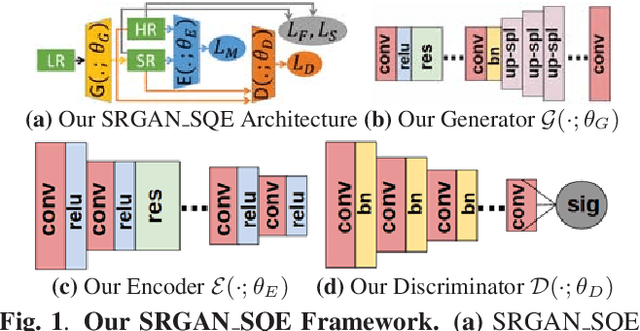
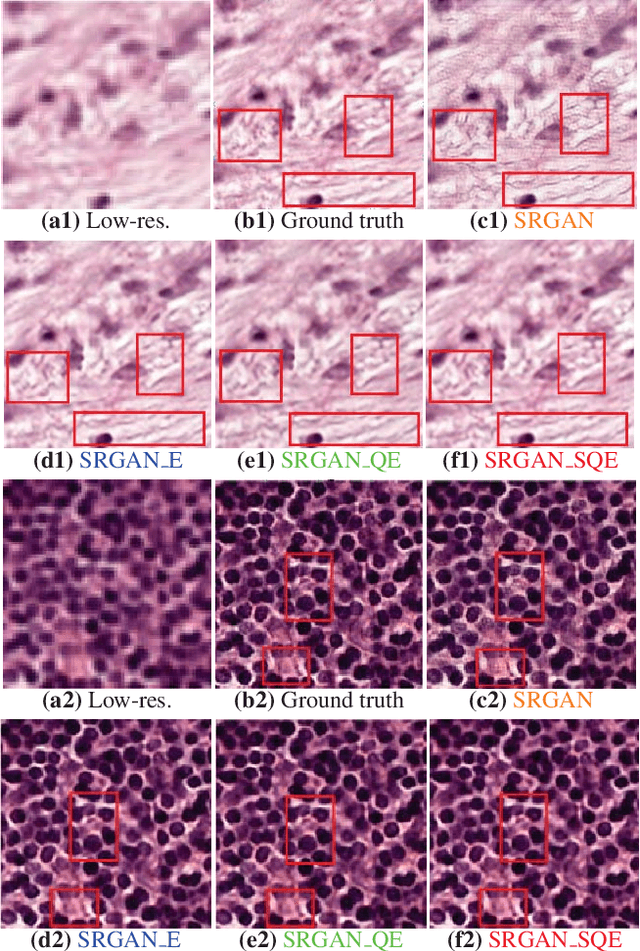
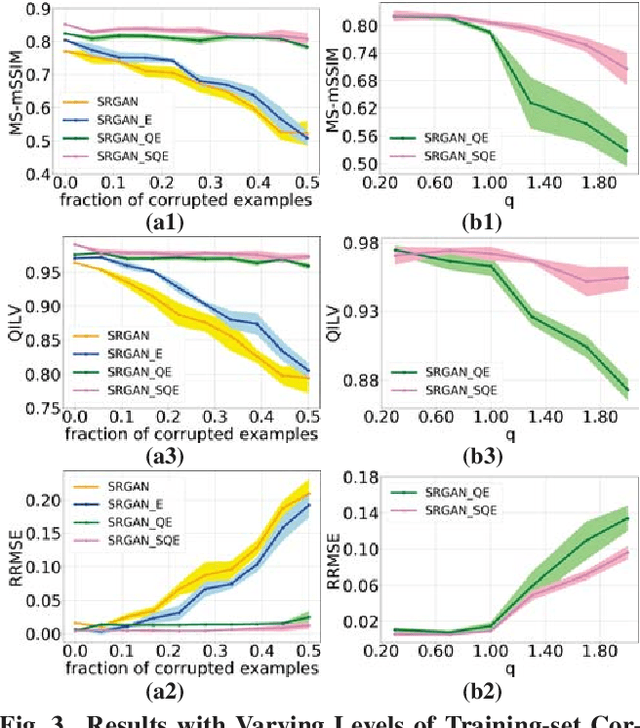
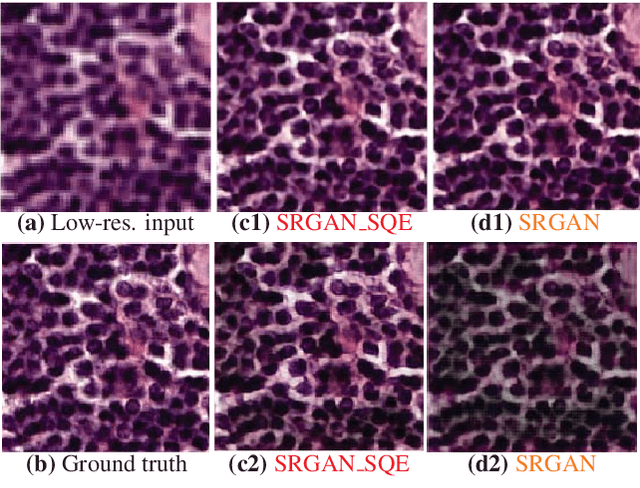
Super-resolution using deep neural networks typically relies on highly curated training sets that are often unavailable in clinical deployment scenarios. Using loss functions that assume Gaussian-distributed residuals makes the learning sensitive to corruptions in clinical training sets. We propose novel loss functions that are robust to corruptions in training sets by modeling heavy-tailed non-Gaussian distributions on the residuals. We propose a loss based on an autoencoder-based manifold-distance between the super-resolved and high-resolution images, to reproduce realistic textural content in super-resolved images. We propose to learn to super-resolve images to match human perceptions of structure, luminance, and contrast. Results on a large clinical dataset shows the advantages of each of our contributions, where our framework improves over the state of the art.

Sparse Kernel PCA for Outlier Detection

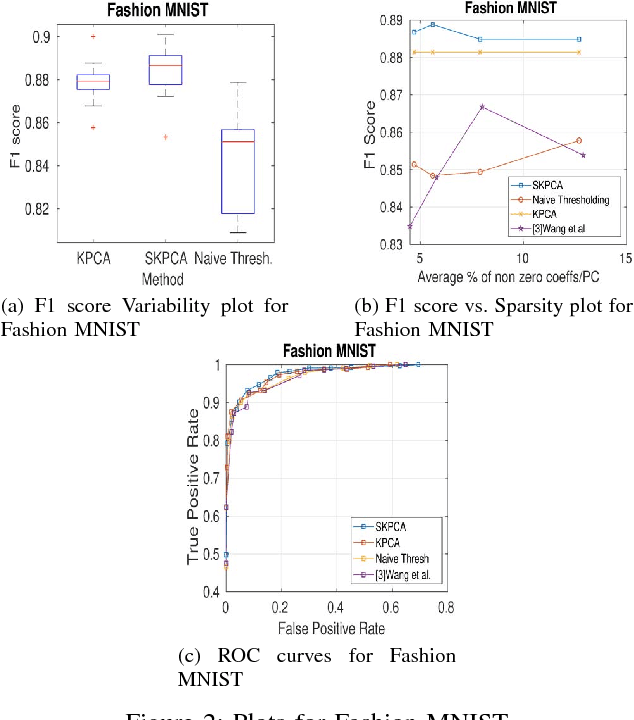
In this paper, we propose a new method to perform Sparse Kernel Principal Component Analysis (SKPCA) and also mathematically analyze the validity of SKPCA. We formulate SKPCA as a constrained optimization problem with elastic net regularization (Hastie et al.) in kernel feature space and solve it. We consider outlier detection (where KPCA is employed) as an application for SKPCA, using the RBF kernel. We test it on 5 real-world datasets and show that by using just 4% (or even less) of the principal components (PCs), where each PC has on average less than 12% non-zero elements in the worst case among all 5 datasets, we are able to nearly match and in 3 datasets even outperform KPCA. We also compare the performance of our method with a recently proposed method for SKPCA by Wang et al. and show that our method performs better in terms of both accuracy and sparsity. We also provide a novel probabilistic proof to justify the existence of sparse solutions for KPCA using the RBF kernel. To the best of our knowledge, this is the first attempt at theoretically analyzing the validity of SKPCA.

Hierarchical Graphical Models for Multigroup Shape Analysis using Expectation Maximization with Sampling in Kendall's Shape Space

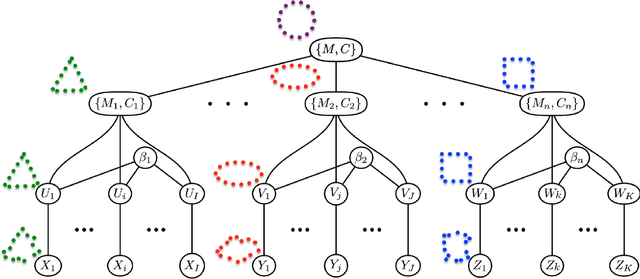
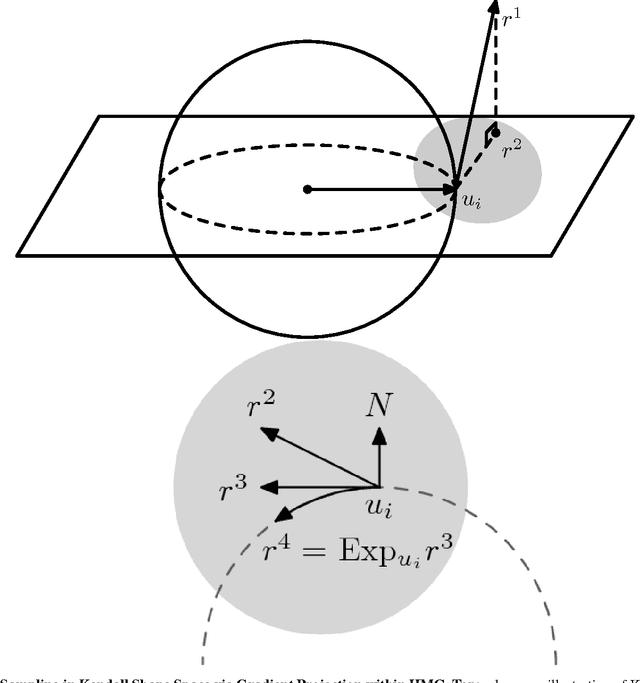
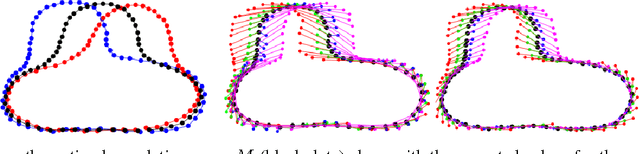
This paper proposes a novel framework for multi-group shape analysis relying on a hierarchical graphical statistical model on shapes within a population.The framework represents individual shapes as point setsmodulo translation, rotation, and scale, following the notion in Kendall shape space.While individual shapes are derived from their group shape model, each group shape model is derived from a single population shape model. The hierarchical model follows the natural organization of population data and the top level in the hierarchy provides a common frame of reference for multigroup shape analysis, e.g. classification and hypothesis testing. Unlike typical shape-modeling approaches, the proposed model is a generative model that defines a joint distribution of object-boundary data and the shape-model variables. Furthermore, it naturally enforces optimal correspondences during the process of model fitting and thereby subsumes the so-called correspondence problem. The proposed inference scheme employs an expectation maximization (EM) algorithm that treats the individual and group shape variables as hidden random variables and integrates them out before estimating the parameters (population mean and variance and the group variances). The underpinning of the EM algorithm is the sampling of pointsets, in Kendall shape space, from their posterior distribution, for which we exploit a highly-efficient scheme based on Hamiltonian Monte Carlo simulation. Experiments in this paper use the fitted hierarchical model to perform (1) hypothesis testing for comparison between pairs of groups using permutation testing and (2) classification for image retrieval. The paper validates the proposed framework on simulated data and demonstrates results on real data.