Sparse Kernel PCA for Outlier Detection
Paper and Code
Sep 13, 2018
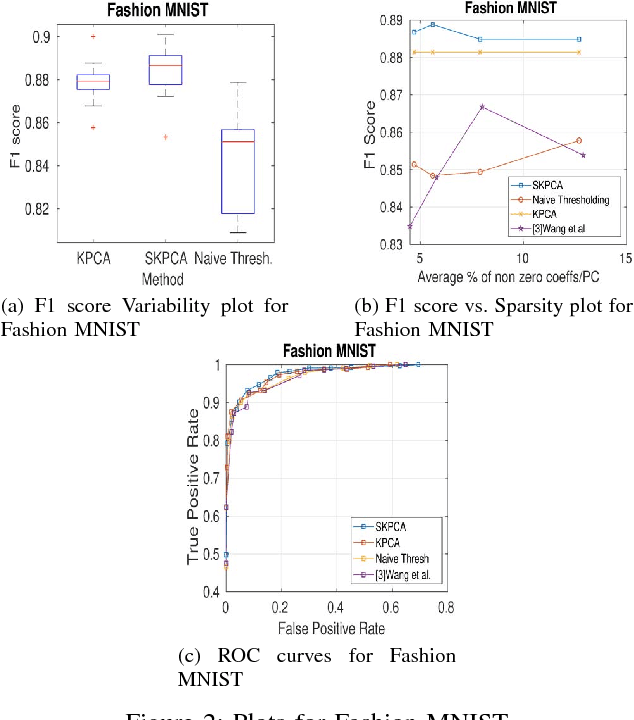


In this paper, we propose a new method to perform Sparse Kernel Principal Component Analysis (SKPCA) and also mathematically analyze the validity of SKPCA. We formulate SKPCA as a constrained optimization problem with elastic net regularization (Hastie et al.) in kernel feature space and solve it. We consider outlier detection (where KPCA is employed) as an application for SKPCA, using the RBF kernel. We test it on 5 real-world datasets and show that by using just 4% (or even less) of the principal components (PCs), where each PC has on average less than 12% non-zero elements in the worst case among all 5 datasets, we are able to nearly match and in 3 datasets even outperform KPCA. We also compare the performance of our method with a recently proposed method for SKPCA by Wang et al. and show that our method performs better in terms of both accuracy and sparsity. We also provide a novel probabilistic proof to justify the existence of sparse solutions for KPCA using the RBF kernel. To the best of our knowledge, this is the first attempt at theoretically analyzing the validity of SKPCA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge