Suhyun Kang
Task-Specific Preconditioner for Cross-Domain Few-Shot Learning
Dec 20, 2024
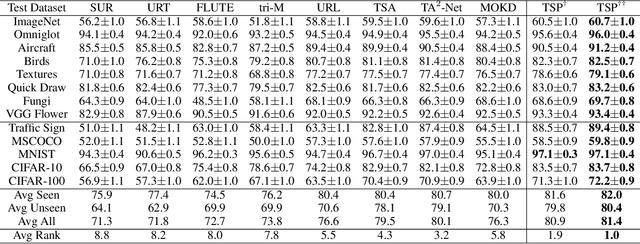
Abstract:Cross-Domain Few-Shot Learning~(CDFSL) methods typically parameterize models with task-agnostic and task-specific parameters. To adapt task-specific parameters, recent approaches have utilized fixed optimization strategies, despite their potential sub-optimality across varying domains or target tasks. To address this issue, we propose a novel adaptation mechanism called Task-Specific Preconditioned gradient descent~(TSP). Our method first meta-learns Domain-Specific Preconditioners~(DSPs) that capture the characteristics of each meta-training domain, which are then linearly combined using task-coefficients to form the Task-Specific Preconditioner. The preconditioner is applied to gradient descent, making the optimization adaptive to the target task. We constrain our preconditioners to be positive definite, guiding the preconditioned gradient toward the direction of steepest descent. Empirical evaluations on the Meta-Dataset show that TSP achieves state-of-the-art performance across diverse experimental scenarios.
Towards a Better Evaluation of Out-of-Domain Generalization
Jun 02, 2024Abstract:The objective of Domain Generalization (DG) is to devise algorithms and models capable of achieving high performance on previously unseen test distributions. In the pursuit of this objective, average measure has been employed as the prevalent measure for evaluating models and comparing algorithms in the existing DG studies. Despite its significance, a comprehensive exploration of the average measure has been lacking and its suitability in approximating the true domain generalization performance has been questionable. In this study, we carefully investigate the limitations inherent in the average measure and propose worst+gap measure as a robust alternative. We establish theoretical grounds of the proposed measure by deriving two theorems starting from two different assumptions. We conduct extensive experimental investigations to compare the proposed worst+gap measure with the conventional average measure. Given the indispensable need to access the true DG performance for studying measures, we modify five existing datasets to come up with SR-CMNIST, C-Cats&Dogs, L-CIFAR10, PACS-corrupted, and VLCS-corrupted datasets. The experiment results unveil an inferior performance of the average measure in approximating the true DG performance and confirm the robustness of the theoretically supported worst+gap measure.
A Differentiable Framework for End-to-End Learning of Hybrid Structured Compression
Sep 21, 2023



Abstract:Filter pruning and low-rank decomposition are two of the foundational techniques for structured compression. Although recent efforts have explored hybrid approaches aiming to integrate the advantages of both techniques, their performance gains have been modest at best. In this study, we develop a \textit{Differentiable Framework~(DF)} that can express filter selection, rank selection, and budget constraint into a single analytical formulation. Within the framework, we introduce DML-S for filter selection, integrating scheduling into existing mask learning techniques. Additionally, we present DTL-S for rank selection, utilizing a singular value thresholding operator. The framework with DML-S and DTL-S offers a hybrid structured compression methodology that facilitates end-to-end learning through gradient-base optimization. Experimental results demonstrate the efficacy of DF, surpassing state-of-the-art structured compression methods. Our work establishes a robust and versatile avenue for advancing structured compression techniques.
Towards a Rigorous Analysis of Mutual Information in Contrastive Learning
Aug 30, 2023



Abstract:Contrastive learning has emerged as a cornerstone in recent achievements of unsupervised representation learning. Its primary paradigm involves an instance discrimination task with a mutual information loss. The loss is known as InfoNCE and it has yielded vital insights into contrastive learning through the lens of mutual information analysis. However, the estimation of mutual information can prove challenging, creating a gap between the elegance of its mathematical foundation and the complexity of its estimation. As a result, drawing rigorous insights or conclusions from mutual information analysis becomes intricate. In this study, we introduce three novel methods and a few related theorems, aimed at enhancing the rigor of mutual information analysis. Despite their simplicity, these methods can carry substantial utility. Leveraging these approaches, we reassess three instances of contrastive learning analysis, illustrating their capacity to facilitate deeper comprehension or to rectify pre-existing misconceptions. Specifically, we investigate small batch size, mutual information as a measure, and the InfoMin principle.
VNE: An Effective Method for Improving Deep Representation by Manipulating Eigenvalue Distribution
Apr 04, 2023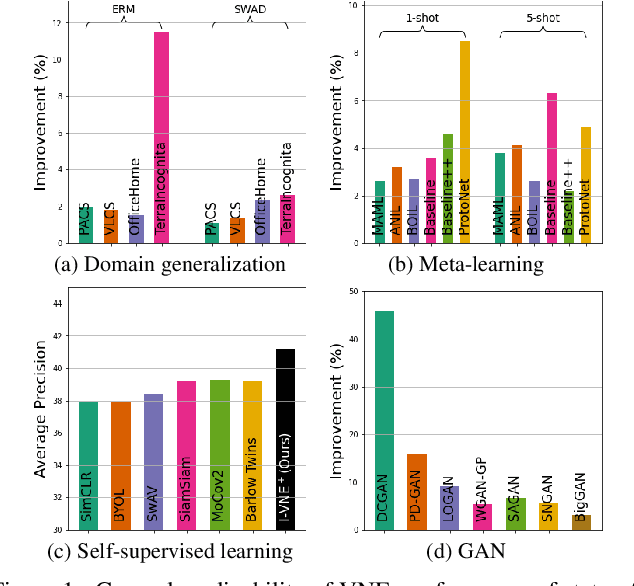
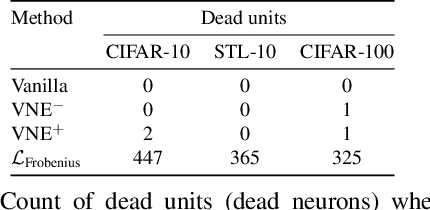
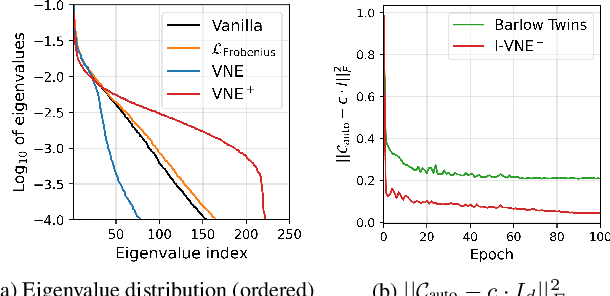
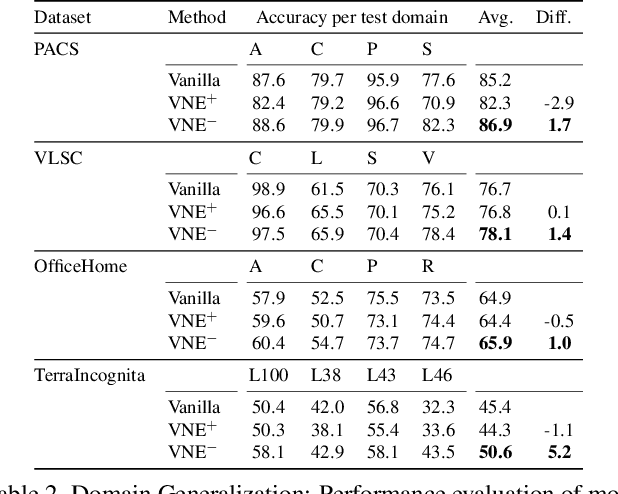
Abstract:Since the introduction of deep learning, a wide scope of representation properties, such as decorrelation, whitening, disentanglement, rank, isotropy, and mutual information, have been studied to improve the quality of representation. However, manipulating such properties can be challenging in terms of implementational effectiveness and general applicability. To address these limitations, we propose to regularize von Neumann entropy~(VNE) of representation. First, we demonstrate that the mathematical formulation of VNE is superior in effectively manipulating the eigenvalues of the representation autocorrelation matrix. Then, we demonstrate that it is widely applicable in improving state-of-the-art algorithms or popular benchmark algorithms by investigating domain-generalization, meta-learning, self-supervised learning, and generative models. In addition, we formally establish theoretical connections with rank, disentanglement, and isotropy of representation. Finally, we provide discussions on the dimension control of VNE and the relationship with Shannon entropy. Code is available at: https://github.com/jaeill/CVPR23-VNE.
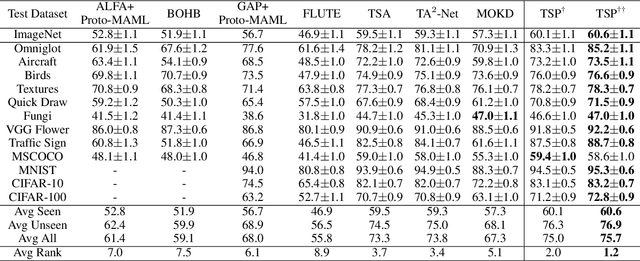
Meta-Learning with a Geometry-Adaptive Preconditioner
Apr 04, 2023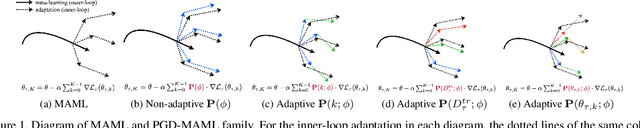

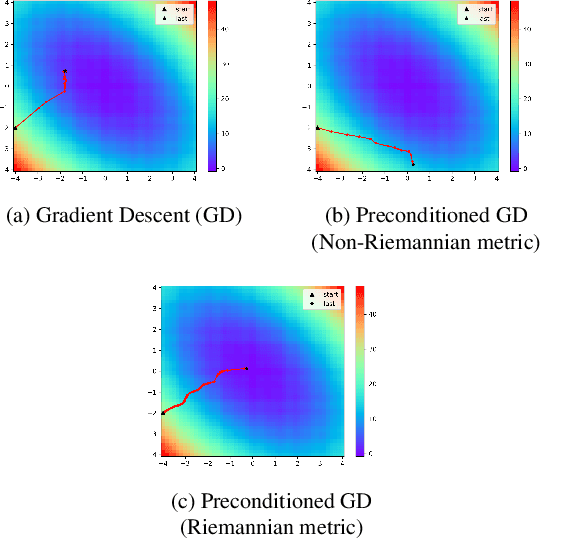
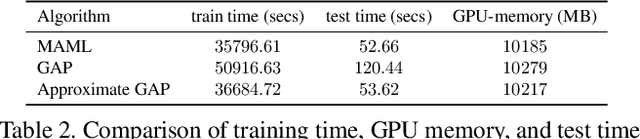
Abstract:Model-agnostic meta-learning (MAML) is one of the most successful meta-learning algorithms. It has a bi-level optimization structure where the outer-loop process learns a shared initialization and the inner-loop process optimizes task-specific weights. Although MAML relies on the standard gradient descent in the inner-loop, recent studies have shown that controlling the inner-loop's gradient descent with a meta-learned preconditioner can be beneficial. Existing preconditioners, however, cannot simultaneously adapt in a task-specific and path-dependent way. Additionally, they do not satisfy the Riemannian metric condition, which can enable the steepest descent learning with preconditioned gradient. In this study, we propose Geometry-Adaptive Preconditioned gradient descent (GAP) that can overcome the limitations in MAML; GAP can efficiently meta-learn a preconditioner that is dependent on task-specific parameters, and its preconditioner can be shown to be a Riemannian metric. Thanks to the two properties, the geometry-adaptive preconditioner is effective for improving the inner-loop optimization. Experiment results show that GAP outperforms the state-of-the-art MAML family and preconditioned gradient descent-MAML (PGD-MAML) family in a variety of few-shot learning tasks. Code is available at: https://github.com/Suhyun777/CVPR23-GAP.
A Highly Effective Low-Rank Compression of Deep Neural Networks with Modified Beam-Search and Modified Stable Rank
Dec 01, 2021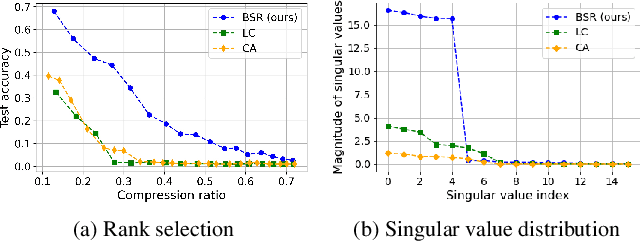
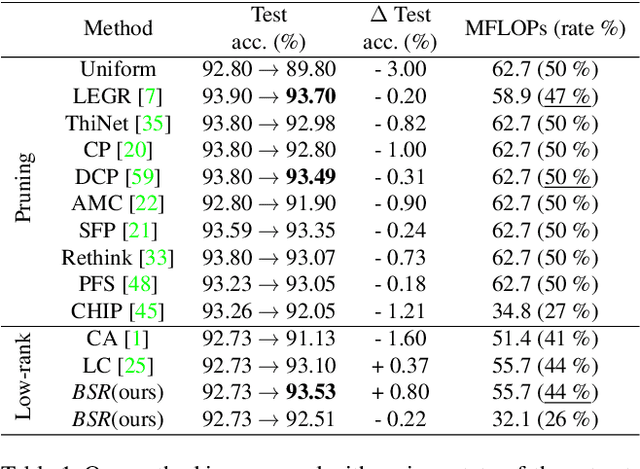
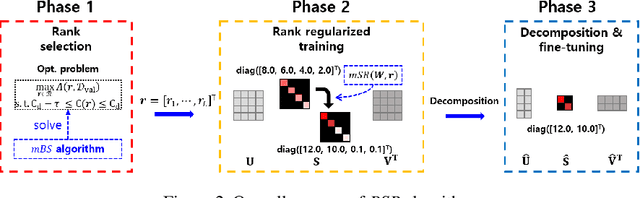

Abstract:Compression has emerged as one of the essential deep learning research topics, especially for the edge devices that have limited computation power and storage capacity. Among the main compression techniques, low-rank compression via matrix factorization has been known to have two problems. First, an extensive tuning is required. Second, the resulting compression performance is typically not impressive. In this work, we propose a low-rank compression method that utilizes a modified beam-search for an automatic rank selection and a modified stable rank for a compression-friendly training. The resulting BSR (Beam-search and Stable Rank) algorithm requires only a single hyperparameter to be tuned for the desired compression ratio. The performance of BSR in terms of accuracy and compression ratio trade-off curve turns out to be superior to the previously known low-rank compression methods. Furthermore, BSR can perform on par with or better than the state-of-the-art structured pruning methods. As with pruning, BSR can be easily combined with quantization for an additional compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge