The co-varying ties between networks and item responses via latent variables

Relationships among teachers are known to influence their teaching-related perceptions. We study whether and how teachers' advising relationships (networks) are related to their perceptions of satisfaction, students, and influence over educational policies, recorded as their responses to a questionnaire (item responses). We propose a novel joint model of network and item responses (JNIRM) with correlated latent variables to understand these co-varying ties. This methodology allows the analyst to test and interpret the dependence between a network and item responses. Using JNIRM, we discover that teachers' advising relationships contribute to their perceptions of satisfaction and students more often than their perceptions of influence over educational policies. In addition, we observe that the complementarity principle applies in certain schools, where teachers tend to seek advice from those who are different from them. JNIRM shows superior parameter estimation and model fit over separately modeling the network and item responses with latent variable models.

VLSI Architectures of Forward Kinematic Processor for Robotics Applications

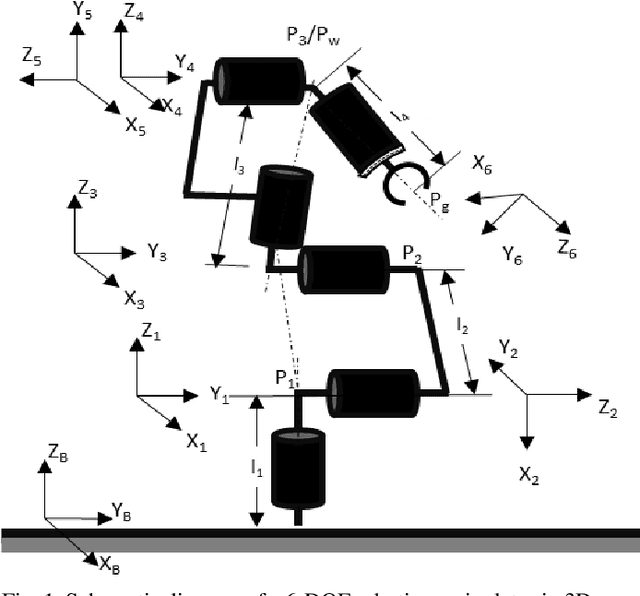
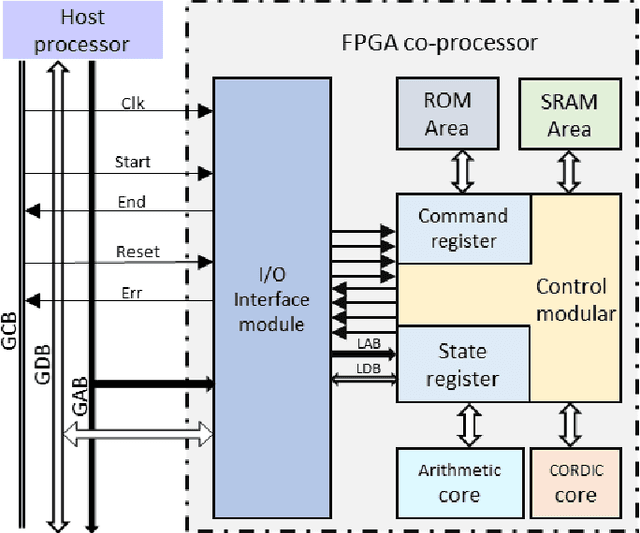
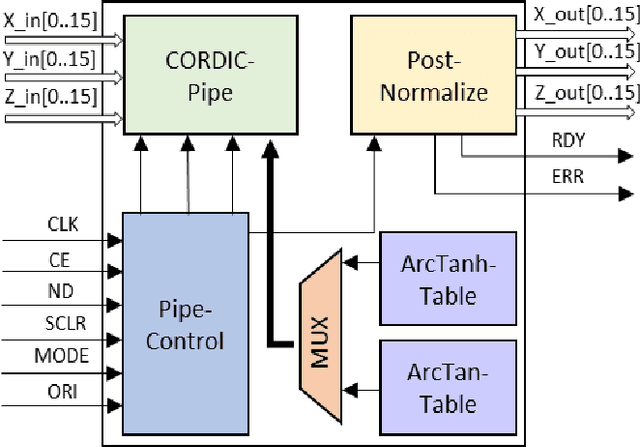
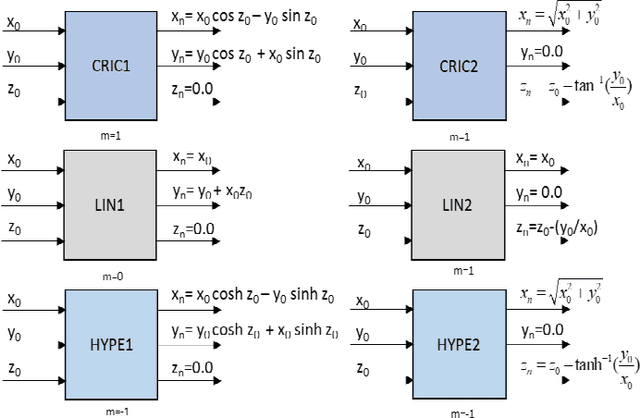
This paper aims to get a comprehensive review of current-day robotic computation technologies at VLSI architecture level. We studied several repots in the domain of robotic processor architecture. In this work, we focused on the forward kinematics architectures which consider CORDIC algorithms, VLSI circuits of WE DSP16 chip, parallel processing and pipelined architecture, and lookup table formula and FPGA processor. This study gives us an understanding of different implementation methods for forward kinematics. Our goal is to develop a forward kinematics processor with FPGA for real-time applications, requires a fast response time and low latency of these devices, useful for industrial automation where the processing speed plays a great role.

A Mutually Exciting Latent Space Hawkes Process Model for Continuous-time Networks

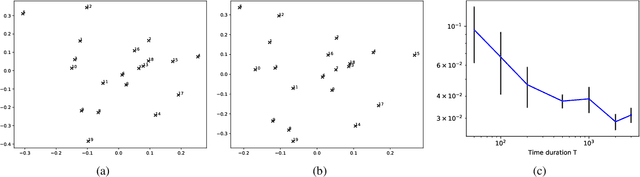
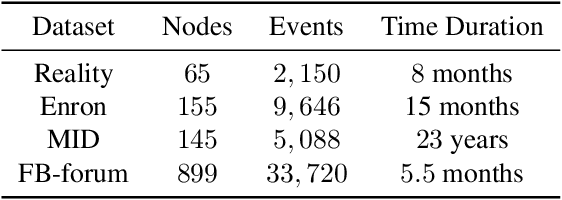
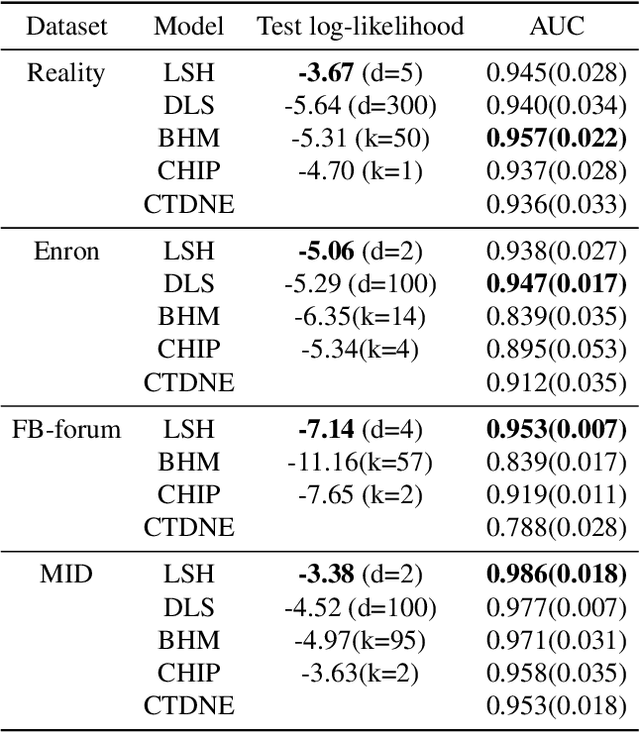
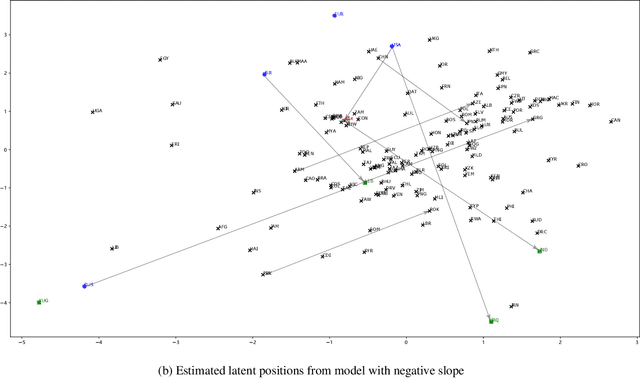
Networks and temporal point processes serve as fundamental building blocks for modeling complex dynamic relational data in various domains. We propose the latent space Hawkes (LSH) model, a novel generative model for continuous-time networks of relational events, using a latent space representation for nodes. We model relational events between nodes using mutually exciting Hawkes processes with baseline intensities dependent upon the distances between the nodes in the latent space and sender and receiver specific effects. We propose an alternating minimization algorithm to jointly estimate the latent positions of the nodes and other model parameters. We demonstrate that our proposed LSH model can replicate many features observed in real temporal networks including reciprocity and transitivity, while also achieves superior prediction accuracy and provides more interpretability compared to existing models.

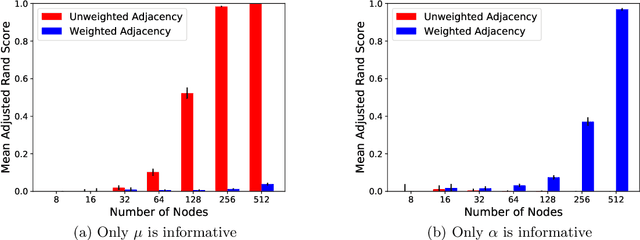
The Multivariate Community Hawkes Model for Dependent Relational Events in Continuous-time Networks

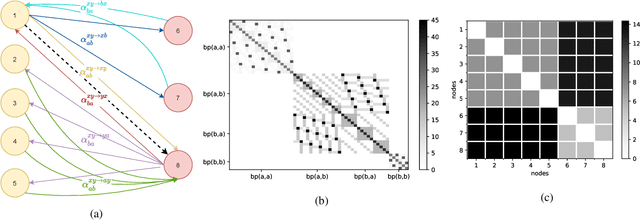
The stochastic block model (SBM) is one of the most widely used generative models for network data. Many continuous-time dynamic network models are built upon the same assumption as the SBM: edges or events between all pairs of nodes are conditionally independent given the block or community memberships, which prevents them from reproducing higher-order motifs such as triangles that are commonly observed in real networks. We propose the multivariate community Hawkes (MULCH) model, an extremely flexible community-based model for continuous-time networks that introduces dependence between node pairs using structured multivariate Hawkes processes. We fit the model using a spectral clustering and likelihood-based local refinement procedure. We find that our proposed MULCH model is far more accurate than existing models both for predictive and generative tasks.

Causal Network Influence with Latent Homophily and Measurement Error: An Application to Therapeutic Community

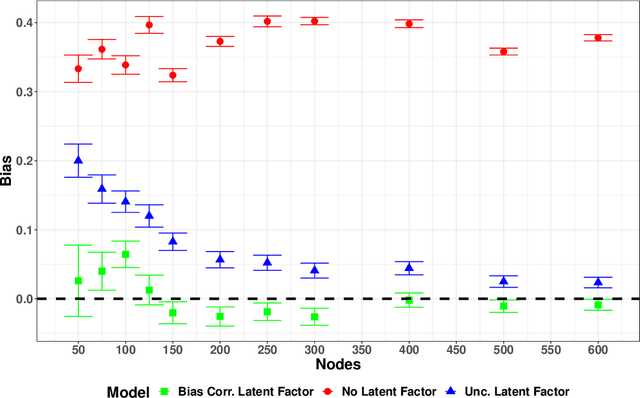
The Spatial or Network Autoregressive model (SAR, NAM) is popular for modeling the influence network connected neighbors exert on the outcome of individuals. However, many authors have noted that the \textit{causal} network influence or contagion cannot be identified from observational data due to the presence of homophily. We propose a latent homophily-adjusted spatial autoregressive model for networked responses to identify the causal contagion and contextual effects. The latent homophily is estimated from the spectral embedding of the network's adjacency matrix. Separately, we develop maximum likelihood estimators for the parameters of the SAR model correcting for measurement error when covariates are measured with error. We show that the bias corrected MLE are consistent and derive its asymptotic limiting distribution. We propose to estimate network influence using the bias corrected MLE in a SAR model with the estimated latent homophily added as a covariate. Our simulations show that the methods perform well in finite sample. We apply our methodology to a data-set of female criminal offenders in a therapeutic community (TC) for substance abuse and criminal behavior. We provide causal estimates of network influence on graduation from TC and re-incarceration after accounting for latent homophily.

Consistent Community Detection in Continuous-Time Networks of Relational Events

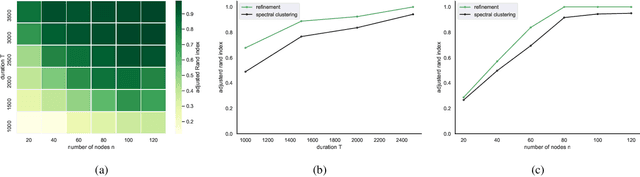
In many application settings involving networks, such as messages between users of an on-line social network or transactions between traders in financial markets, the observed data are in the form of relational events with timestamps, which form a continuous-time network. We propose the Community Hawkes Independent Pairs (CHIP) model for community detection on such timestamped relational event data. We demonstrate that applying spectral clustering to adjacency matrices constructed from relational events generated by the CHIP model provides consistent community detection for a growing number of nodes. In particular, we obtain explicit non-asymptotic upper bounds on the misclustering rates based on the separation conditions required on the parameters of the model for consistent community detection. We also develop consistent and computationally efficient estimators for the parameters of the model. We demonstrate that our proposed CHIP model and estimation procedure scales to large networks with tens of thousands of nodes and provides superior fits compared to existing continuous-time network models on several real networks.

Higher-Order Spectral Clustering under Superimposed Stochastic Block Model

Higher-order motif structures and multi-vertex interactions are becoming increasingly important in studies that aim to improve our understanding of functionalities and evolution patterns of networks. To elucidate the role of higher-order structures in community detection problems over complex networks, we introduce the notion of a Superimposed Stochastic Block Model (SupSBM). The model is based on a random graph framework in which certain higher-order structures or subgraphs are generated through an independent hyperedge generation process, and are then replaced with graphs that are superimposed with directed or undirected edges generated by an inhomogeneous random graph model. Consequently, the model introduces controlled dependencies between edges which allow for capturing more realistic network phenomena, namely strong local clustering in a sparse network, short average path length, and community structure. We proceed to rigorously analyze the performance of a number of recently proposed higher-order spectral clustering methods on the SupSBM. In particular, we prove non-asymptotic upper bounds on the misclustering error of spectral community detection for a SupSBM setting in which triangles or 3-uniform hyperedges are superimposed with undirected edges. As part of our analysis, we also derive new bounds on the misclustering error of higher-order spectral clustering methods for the standard SBM and the 3-uniform hypergraph SBM. Furthermore, for a non-uniform hypergraph SBM model in which one directly observes both edges and 3-uniform hyperedges, we obtain a criterion that describes when to perform spectral clustering based on edges and when on hyperedges, based on a function of hyperedge density and observation quality.

Consistency of community detection in multi-layer networks using spectral and matrix factorization methods

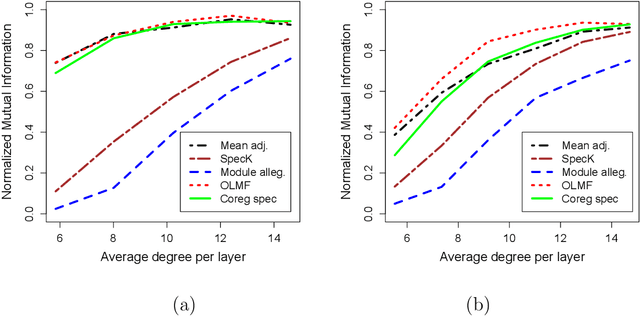
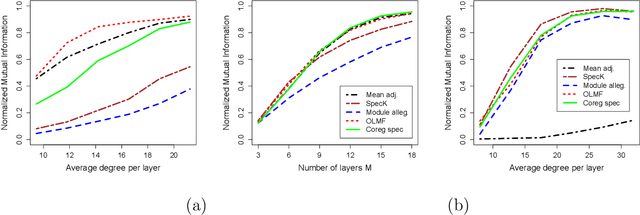
We consider the problem of estimating a consensus community structure by combining information from multiple layers of a multi-layer network or multiple snapshots of a time-varying network. Numerous methods have been proposed in the literature for the more general problem of multi-view clustering in the past decade based on the spectral clustering or a low-rank matrix factorization. As a general theme, these "intermediate fusion" methods involve obtaining a low column rank matrix by optimizing an objective function and then using the columns of the matrix for clustering. However, the theoretical properties of these methods remain largely unexplored and most researchers have relied on the performance in synthetic and real data to assess the goodness of the procedures. In the absence of statistical guarantees on the objective functions, it is difficult to determine if the algorithms optimizing the objective will return a good community structure. We apply some of these methods for consensus community detection in multi-layer networks and investigate the consistency properties of the global optimizer of the objective functions under the multi-layer stochastic blockmodel. We derive several new asymptotic results showing consistency of the intermediate fusion techniques along with the spectral clustering of mean adjacency matrix under a high dimensional setup, where the number of nodes, the number of layers and the number of communities of the multi-layer graph grow. Our numerical study shows that in comparison to the intermediate fusion techniques, late fusion methods, namely spectral clustering on aggregate spectral kernel and module allegiance matrix, under-perform in sparse networks, while the spectral clustering of mean adjacency matrix under-performs in multi-layer networks that contain layers with both homophilic and heterophilic clusters.

Orthogonal symmetric non-negative matrix factorization under the stochastic block model

We present a method based on the orthogonal symmetric non-negative matrix tri-factorization of the normalized Laplacian matrix for community detection in complex networks. While the exact factorization of a given order may not exist and is NP hard to compute, we obtain an approximate factorization by solving an optimization problem. We establish the connection of the factors obtained through the factorization to a non-negative basis of an invariant subspace of the estimated matrix, drawing parallel with the spectral clustering. Using such factorization for clustering in networks is motivated by analyzing a block-diagonal Laplacian matrix with the blocks representing the connected components of a graph. The method is shown to be consistent for community detection in graphs generated from the stochastic block model and the degree corrected stochastic block model. Simulation results and real data analysis show the effectiveness of these methods under a wide variety of situations, including sparse and highly heterogeneous graphs where the usual spectral clustering is known to fail. Our method also performs better than the state of the art in popular benchmark network datasets, e.g., the political web blogs and the karate club data.

Community detection in multi-relational data with restricted multi-layer stochastic blockmodel

In recent years there has been an increased interest in statistical analysis of data with multiple types of relations among a set of entities. Such multi-relational data can be represented as multi-layer graphs where the set of vertices represents the entities and multiple types of edges represent the different relations among them. For community detection in multi-layer graphs, we consider two random graph models, the multi-layer stochastic blockmodel (MLSBM) and a model with a restricted parameter space, the restricted multi-layer stochastic blockmodel (RMLSBM). We derive consistency results for community assignments of the maximum likelihood estimators (MLEs) in both models where MLSBM is assumed to be the true model, and either the number of nodes or the number of types of edges or both grow. We compare MLEs in the two models with other baseline approaches, such as separate modeling of layers, aggregating the layers and majority voting. RMLSBM is shown to have advantage over MLSBM when either the growth rate of the number of communities is high or the growth rate of the average degree of the component graphs in the multi-graph is low. We also derive minimax rates of error and sharp thresholds for achieving consistency of community detection in both models, which are then used to compare the multi-layer models with a baseline model, the aggregate stochastic block model. The simulation studies and real data applications confirm the superior performance of the multi-layer approaches in comparison to the baseline procedures.