Higher-Order Spectral Clustering under Superimposed Stochastic Block Model

Higher-order motif structures and multi-vertex interactions are becoming increasingly important in studies that aim to improve our understanding of functionalities and evolution patterns of networks. To elucidate the role of higher-order structures in community detection problems over complex networks, we introduce the notion of a Superimposed Stochastic Block Model (SupSBM). The model is based on a random graph framework in which certain higher-order structures or subgraphs are generated through an independent hyperedge generation process, and are then replaced with graphs that are superimposed with directed or undirected edges generated by an inhomogeneous random graph model. Consequently, the model introduces controlled dependencies between edges which allow for capturing more realistic network phenomena, namely strong local clustering in a sparse network, short average path length, and community structure. We proceed to rigorously analyze the performance of a number of recently proposed higher-order spectral clustering methods on the SupSBM. In particular, we prove non-asymptotic upper bounds on the misclustering error of spectral community detection for a SupSBM setting in which triangles or 3-uniform hyperedges are superimposed with undirected edges. As part of our analysis, we also derive new bounds on the misclustering error of higher-order spectral clustering methods for the standard SBM and the 3-uniform hypergraph SBM. Furthermore, for a non-uniform hypergraph SBM model in which one directly observes both edges and 3-uniform hyperedges, we obtain a criterion that describes when to perform spectral clustering based on edges and when on hyperedges, based on a function of hyperedge density and observation quality.

Consistency of community detection in multi-layer networks using spectral and matrix factorization methods

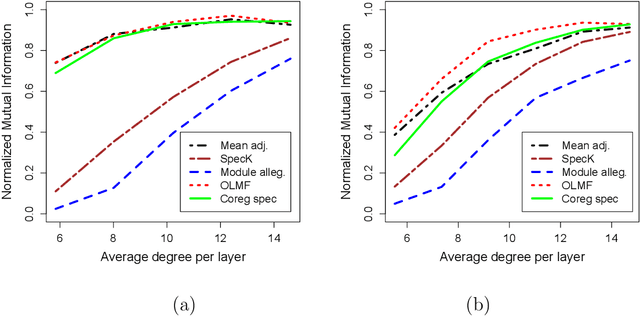
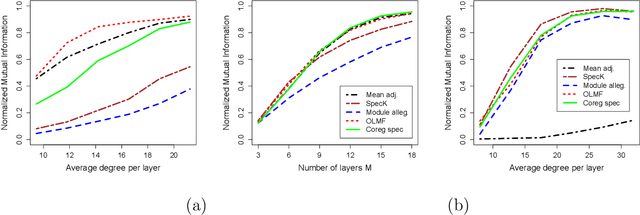
We consider the problem of estimating a consensus community structure by combining information from multiple layers of a multi-layer network or multiple snapshots of a time-varying network. Numerous methods have been proposed in the literature for the more general problem of multi-view clustering in the past decade based on the spectral clustering or a low-rank matrix factorization. As a general theme, these "intermediate fusion" methods involve obtaining a low column rank matrix by optimizing an objective function and then using the columns of the matrix for clustering. However, the theoretical properties of these methods remain largely unexplored and most researchers have relied on the performance in synthetic and real data to assess the goodness of the procedures. In the absence of statistical guarantees on the objective functions, it is difficult to determine if the algorithms optimizing the objective will return a good community structure. We apply some of these methods for consensus community detection in multi-layer networks and investigate the consistency properties of the global optimizer of the objective functions under the multi-layer stochastic blockmodel. We derive several new asymptotic results showing consistency of the intermediate fusion techniques along with the spectral clustering of mean adjacency matrix under a high dimensional setup, where the number of nodes, the number of layers and the number of communities of the multi-layer graph grow. Our numerical study shows that in comparison to the intermediate fusion techniques, late fusion methods, namely spectral clustering on aggregate spectral kernel and module allegiance matrix, under-perform in sparse networks, while the spectral clustering of mean adjacency matrix under-performs in multi-layer networks that contain layers with both homophilic and heterophilic clusters.

Orthogonal symmetric non-negative matrix factorization under the stochastic block model

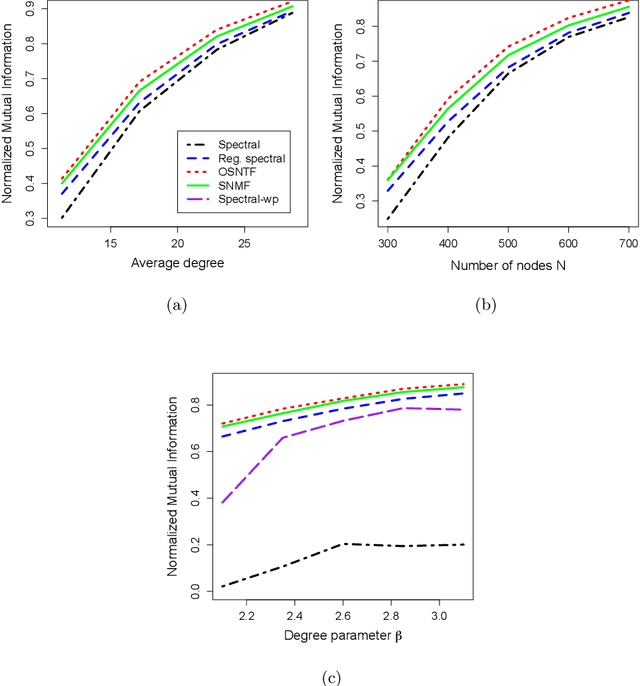
We present a method based on the orthogonal symmetric non-negative matrix tri-factorization of the normalized Laplacian matrix for community detection in complex networks. While the exact factorization of a given order may not exist and is NP hard to compute, we obtain an approximate factorization by solving an optimization problem. We establish the connection of the factors obtained through the factorization to a non-negative basis of an invariant subspace of the estimated matrix, drawing parallel with the spectral clustering. Using such factorization for clustering in networks is motivated by analyzing a block-diagonal Laplacian matrix with the blocks representing the connected components of a graph. The method is shown to be consistent for community detection in graphs generated from the stochastic block model and the degree corrected stochastic block model. Simulation results and real data analysis show the effectiveness of these methods under a wide variety of situations, including sparse and highly heterogeneous graphs where the usual spectral clustering is known to fail. Our method also performs better than the state of the art in popular benchmark network datasets, e.g., the political web blogs and the karate club data.

Community detection in multi-relational data with restricted multi-layer stochastic blockmodel

In recent years there has been an increased interest in statistical analysis of data with multiple types of relations among a set of entities. Such multi-relational data can be represented as multi-layer graphs where the set of vertices represents the entities and multiple types of edges represent the different relations among them. For community detection in multi-layer graphs, we consider two random graph models, the multi-layer stochastic blockmodel (MLSBM) and a model with a restricted parameter space, the restricted multi-layer stochastic blockmodel (RMLSBM). We derive consistency results for community assignments of the maximum likelihood estimators (MLEs) in both models where MLSBM is assumed to be the true model, and either the number of nodes or the number of types of edges or both grow. We compare MLEs in the two models with other baseline approaches, such as separate modeling of layers, aggregating the layers and majority voting. RMLSBM is shown to have advantage over MLSBM when either the growth rate of the number of communities is high or the growth rate of the average degree of the component graphs in the multi-graph is low. We also derive minimax rates of error and sharp thresholds for achieving consistency of community detection in both models, which are then used to compare the multi-layer models with a baseline model, the aggregate stochastic block model. The simulation studies and real data applications confirm the superior performance of the multi-layer approaches in comparison to the baseline procedures.