Consistency of community detection in multi-layer networks using spectral and matrix factorization methods

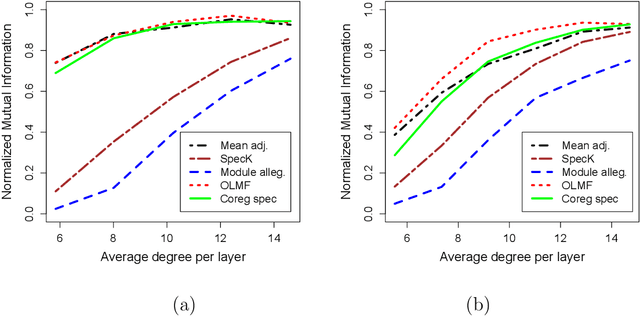
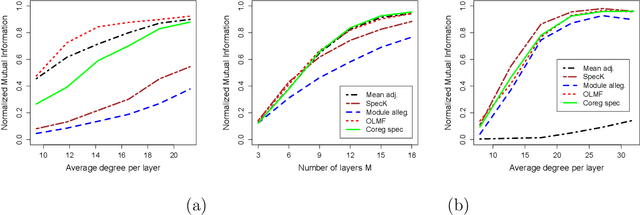
We consider the problem of estimating a consensus community structure by combining information from multiple layers of a multi-layer network or multiple snapshots of a time-varying network. Numerous methods have been proposed in the literature for the more general problem of multi-view clustering in the past decade based on the spectral clustering or a low-rank matrix factorization. As a general theme, these "intermediate fusion" methods involve obtaining a low column rank matrix by optimizing an objective function and then using the columns of the matrix for clustering. However, the theoretical properties of these methods remain largely unexplored and most researchers have relied on the performance in synthetic and real data to assess the goodness of the procedures. In the absence of statistical guarantees on the objective functions, it is difficult to determine if the algorithms optimizing the objective will return a good community structure. We apply some of these methods for consensus community detection in multi-layer networks and investigate the consistency properties of the global optimizer of the objective functions under the multi-layer stochastic blockmodel. We derive several new asymptotic results showing consistency of the intermediate fusion techniques along with the spectral clustering of mean adjacency matrix under a high dimensional setup, where the number of nodes, the number of layers and the number of communities of the multi-layer graph grow. Our numerical study shows that in comparison to the intermediate fusion techniques, late fusion methods, namely spectral clustering on aggregate spectral kernel and module allegiance matrix, under-perform in sparse networks, while the spectral clustering of mean adjacency matrix under-performs in multi-layer networks that contain layers with both homophilic and heterophilic clusters.