Spectral clustering for dependent community Hawkes process models of temporal networks

Temporal networks observed continuously over time through timestamped relational events data are commonly encountered in application settings including online social media communications, financial transactions, and international relations. Temporal networks often exhibit community structure and strong dependence patterns among node pairs. This dependence can be modeled through mutual excitations, where an interaction event from a sender to a receiver node increases the possibility of future events among other node pairs. We provide statistical results for a class of models that we call dependent community Hawkes (DCH) models, which combine the stochastic block model with mutually exciting Hawkes processes for modeling both community structure and dependence among node pairs, respectively. We derive a non-asymptotic upper bound on the misclustering error of spectral clustering on the event count matrix as a function of the number of nodes and communities, time duration, and the amount of dependence in the model. Our result leverages recent results on bounding an appropriate distance between a multivariate Hawkes process count vector and a Gaussian vector, along with results from random matrix theory. We also propose a DCH model that incorporates only self and reciprocal excitation along with highly scalable parameter estimation using a Generalized Method of Moments (GMM) estimator that we demonstrate to be consistent for growing network size and time duration.

A Mutually Exciting Latent Space Hawkes Process Model for Continuous-time Networks

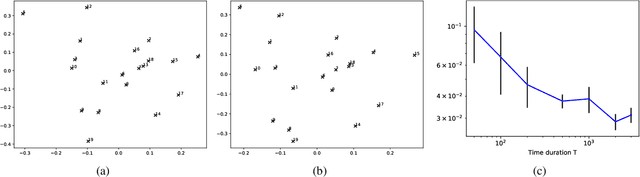
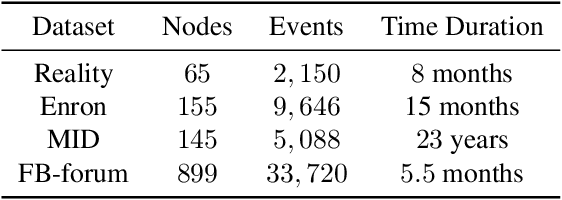
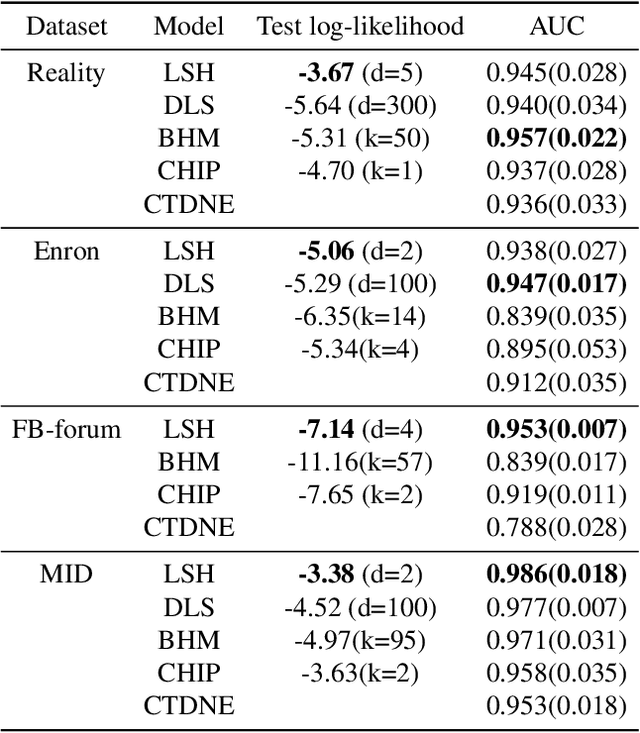
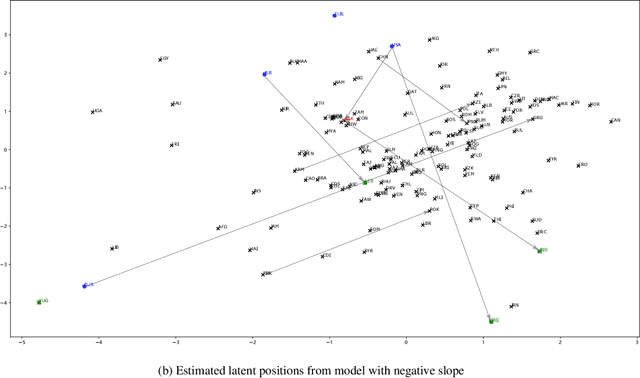
Networks and temporal point processes serve as fundamental building blocks for modeling complex dynamic relational data in various domains. We propose the latent space Hawkes (LSH) model, a novel generative model for continuous-time networks of relational events, using a latent space representation for nodes. We model relational events between nodes using mutually exciting Hawkes processes with baseline intensities dependent upon the distances between the nodes in the latent space and sender and receiver specific effects. We propose an alternating minimization algorithm to jointly estimate the latent positions of the nodes and other model parameters. We demonstrate that our proposed LSH model can replicate many features observed in real temporal networks including reciprocity and transitivity, while also achieves superior prediction accuracy and provides more interpretability compared to existing models.

The Multivariate Community Hawkes Model for Dependent Relational Events in Continuous-time Networks

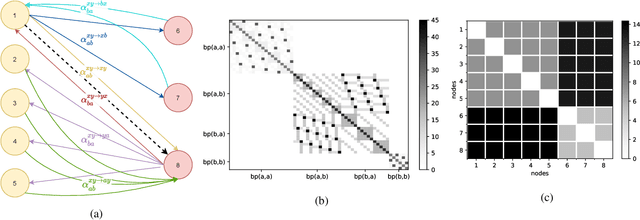
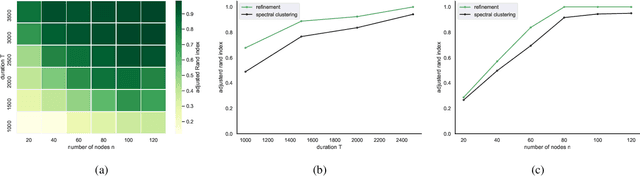
The stochastic block model (SBM) is one of the most widely used generative models for network data. Many continuous-time dynamic network models are built upon the same assumption as the SBM: edges or events between all pairs of nodes are conditionally independent given the block or community memberships, which prevents them from reproducing higher-order motifs such as triangles that are commonly observed in real networks. We propose the multivariate community Hawkes (MULCH) model, an extremely flexible community-based model for continuous-time networks that introduces dependence between node pairs using structured multivariate Hawkes processes. We fit the model using a spectral clustering and likelihood-based local refinement procedure. We find that our proposed MULCH model is far more accurate than existing models both for predictive and generative tasks.