Hyperspectral Image Spectral-Spatial Feature Extraction via Tensor Principal Component Analysis

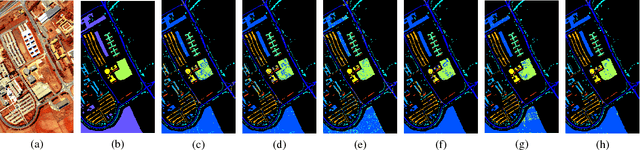
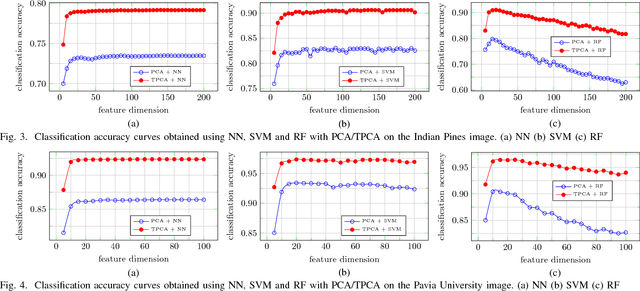
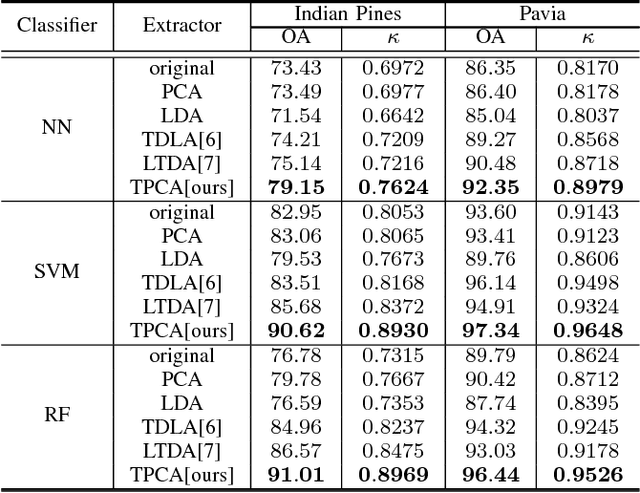
This paper addresses the challenge of spectral-spatial feature extraction for hyperspectral image classification by introducing a novel tensor-based framework. The proposed approach incorporates circular convolution into a tensor structure to effectively capture and integrate both spectral and spatial information. Building upon this framework, the traditional Principal Component Analysis (PCA) technique is extended to its tensor-based counterpart, referred to as Tensor Principal Component Analysis (TPCA). The proposed TPCA method leverages the inherent multi-dimensional structure of hyperspectral data, thereby enabling more effective feature representation. Experimental results on benchmark hyperspectral datasets demonstrate that classification models using TPCA features consistently outperform those using traditional PCA and other state-of-the-art techniques. These findings highlight the potential of the tensor-based framework in advancing hyperspectral image analysis.

General Data Analytics with Applications to Visual Information Analysis: A Provable Backward-Compatible Semisimple Paradigm over T-Algebra

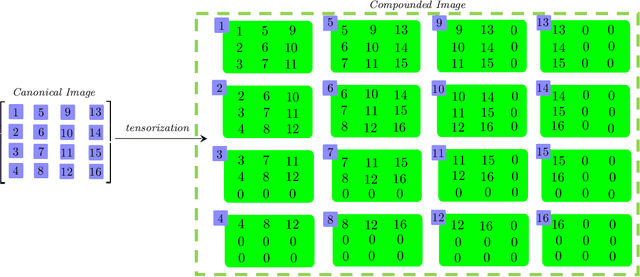
We consider a novel backward-compatible paradigm of general data analytics over a recently-reported semisimple algebra (called t-algebra). We study the abstract algebraic framework over the t-algebra by representing the elements of t-algebra by fix-sized multi-way arrays of complex numbers and the algebraic structure over the t-algebra by a collection of direct-product constituents. Over the t-algebra, many algorithms, if not all, are generalized in a straightforward manner using this new semisimple paradigm. To demonstrate the new paradigm's performance and its backward-compatibility, we generalize some canonical algorithms for visual pattern analysis. Experiments on public datasets show that the generalized algorithms compare favorably with their canonical counterparts.

Knowledge Distillation: A Survey

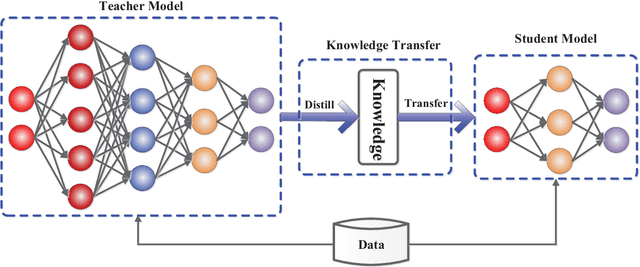
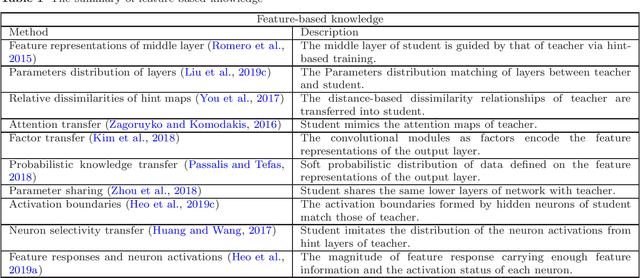
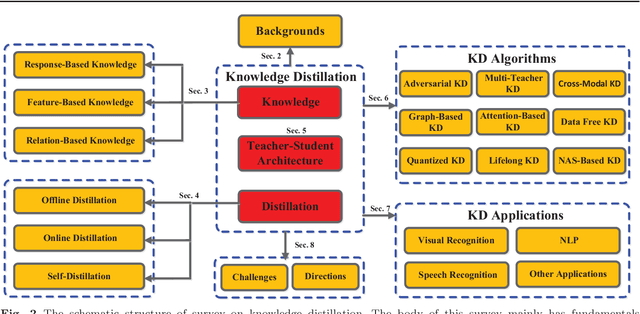
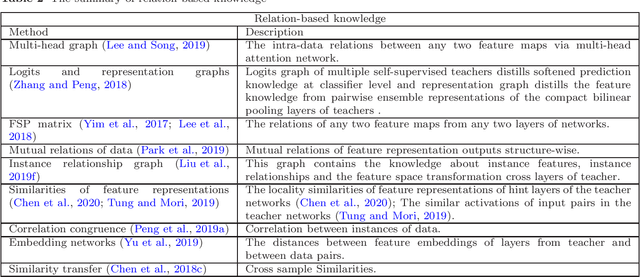
In recent years, deep neural networks have been successful in both industry and academia, especially for computer vision tasks. The great success of deep learning is mainly due to its scalability to encode large-scale data and to maneuver billions of model parameters. However, it is a challenge to deploy these cumbersome deep models on devices with limited resources, e.g., mobile phones and embedded devices, not only because of the high computational complexity but also the large storage requirements. To this end, a variety of model compression and acceleration techniques have been developed. As a representative type of model compression and acceleration, knowledge distillation effectively learns a small student model from a large teacher model. It has received rapid increasing attention from the community. This paper provides a comprehensive survey of knowledge distillation from the perspectives of knowledge categories, training schemes, distillation algorithms and applications. Furthermore, challenges in knowledge distillation are briefly reviewed and comments on future research are discussed and forwarded.

Intrinsic Dimension Estimation via Nearest Constrained Subspace Classifier

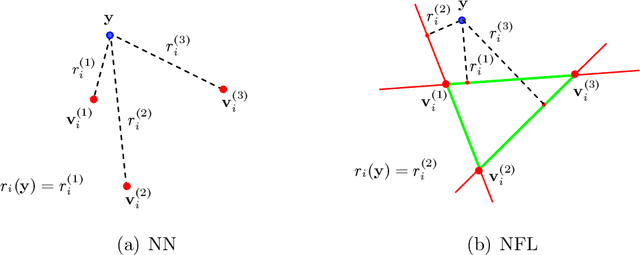
We consider the problems of classification and intrinsic dimension estimation on image data. A new subspace based classifier is proposed for supervised classification or intrinsic dimension estimation. The distribution of the data in each class is modeled by a union of of a finite number ofaffine subspaces of the feature space. The affine subspaces have a common dimension, which is assumed to be much less than the dimension of the feature space. The subspaces are found using regression based on the L0-norm. The proposed method is a generalisation of classical NN (Nearest Neighbor), NFL (Nearest Feature Line) classifiers and has a close relationship to NS (Nearest Subspace) classifier. The proposed classifier with an accurately estimated dimension parameter generally outperforms its competitors in terms of classification accuracy. We also propose a fast version of the classifier using a neighborhood representation to reduce its computational complexity. Experiments on publicly available datasets corroborate these claims.

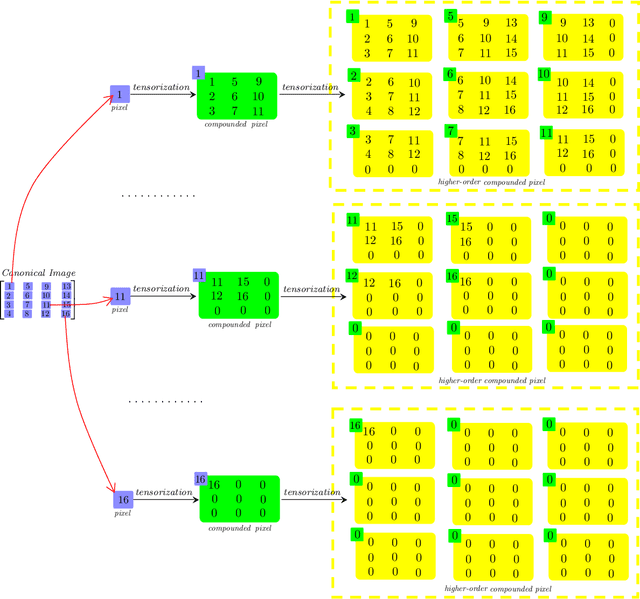
Generalized Visual Information Analysis via Tensorial Algebra

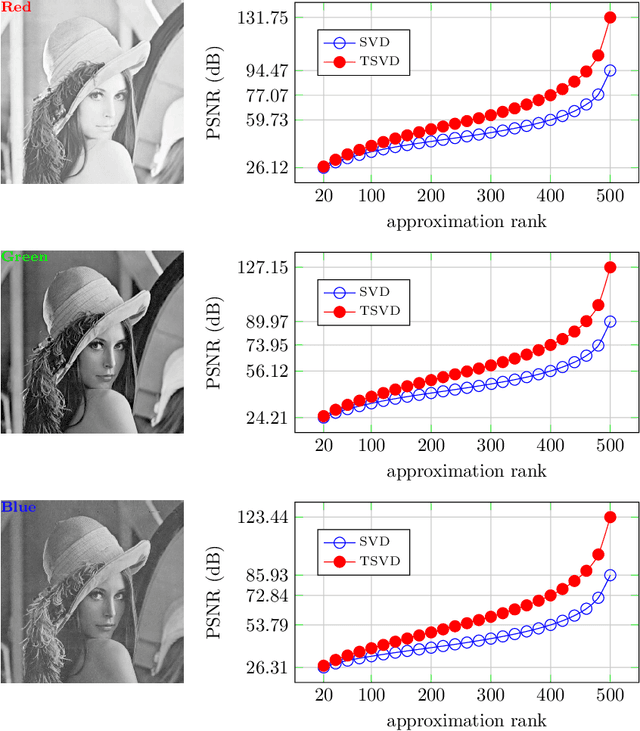
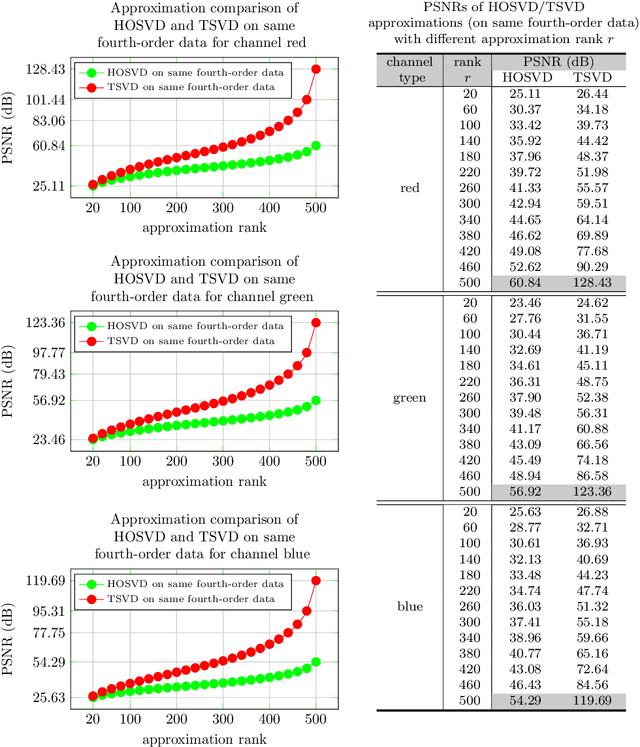
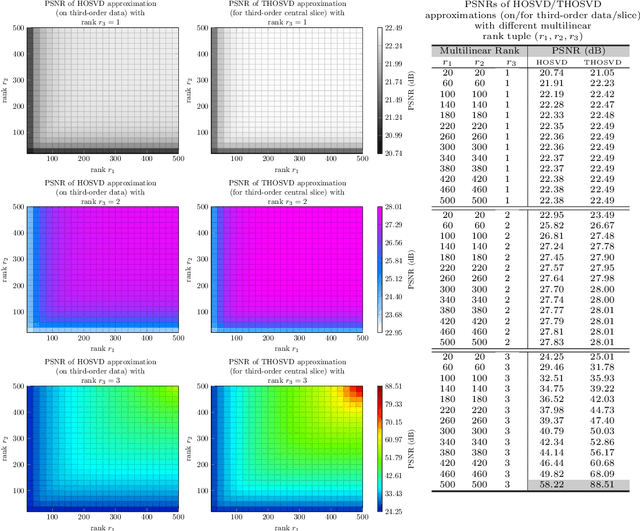
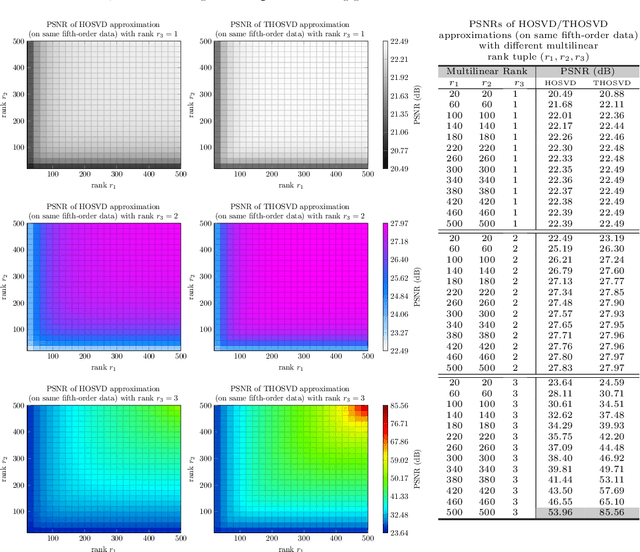
High order data is modeled using matrices whose entries are numerical arrays of a fixed size. These arrays, called t-scalars, form a commutative ring under the convolution product. Matrices with elements in the ring of t-scalars are referred to as t-matrices. The t-matrices can be scaled, added and multiplied in the usual way. There are t-matrix generalizations of positive matrices, orthogonal matrices and Hermitian symmetric matrices. With the t-matrix model, it is possible to generalize many well-known matrix algorithms. In particular, the t-matrices are used to generalize the SVD (Singular Value Decomposition), HOSVD (High Order SVD), PCA (Principal Component Analysis), 2DPCA (Two Dimensional PCA) and GCA (Grassmannian Component Analysis). The generalized t-matrix algorithms, namely TSVD, THOSVD,TPCA, T2DPCA and TGCA, are applied to low-rank approximation, reconstruction,and supervised classification of images. Experiments show that the t-matrix algorithms compare favorably with standard matrix algorithms.