General Data Analytics with Applications to Visual Information Analysis: A Provable Backward-Compatible Semisimple Paradigm over T-Algebra
Paper and Code
Nov 16, 2020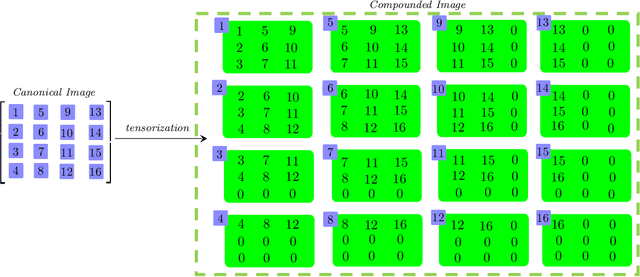
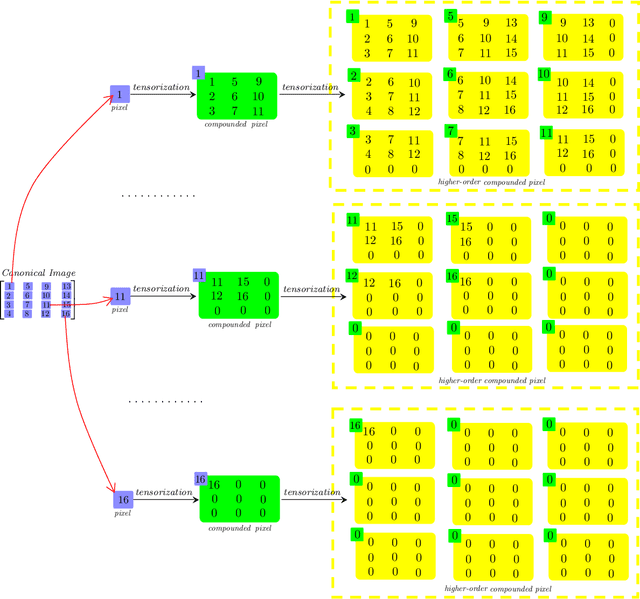


We consider a novel backward-compatible paradigm of general data analytics over a recently-reported semisimple algebra (called t-algebra). We study the abstract algebraic framework over the t-algebra by representing the elements of t-algebra by fix-sized multi-way arrays of complex numbers and the algebraic structure over the t-algebra by a collection of direct-product constituents. Over the t-algebra, many algorithms, if not all, are generalized in a straightforward manner using this new semisimple paradigm. To demonstrate the new paradigm's performance and its backward-compatibility, we generalize some canonical algorithms for visual pattern analysis. Experiments on public datasets show that the generalized algorithms compare favorably with their canonical counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge