Online Convex Optimization of Programmable Quantum Computers to Simulate Time-Varying Quantum Channels

Simulating quantum channels is a fundamental primitive in quantum computing, since quantum channels define general (trace-preserving) quantum operations. An arbitrary quantum channel cannot be exactly simulated using a finite-dimensional programmable quantum processor, making it important to develop optimal approximate simulation techniques. In this paper, we study the challenging setting in which the channel to be simulated varies adversarially with time. We propose the use of matrix exponentiated gradient descent (MEGD), an online convex optimization method, and analytically show that it achieves a sublinear regret in time. Through experiments, we validate the main results for time-varying dephasing channels using a programmable generalized teleportation processor.

Generalization in Quantum Machine Learning: a Quantum Information Perspective

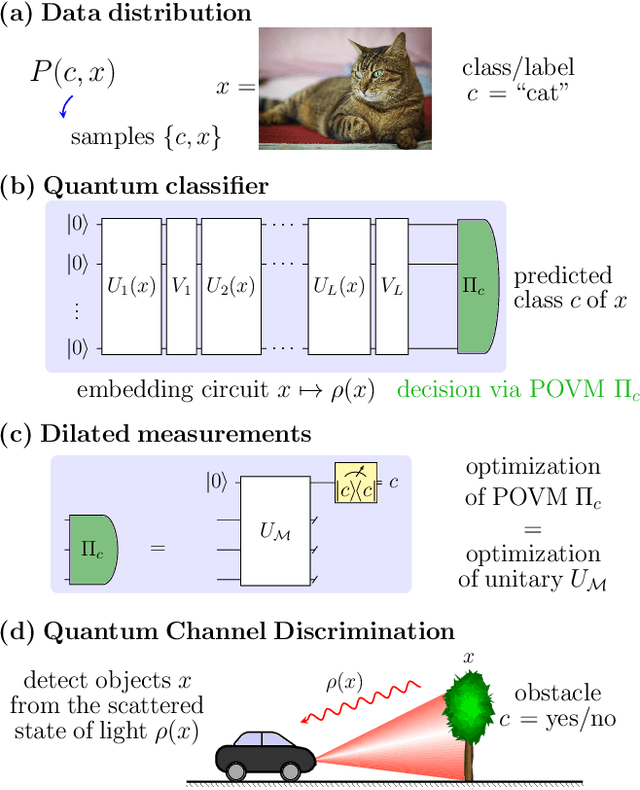
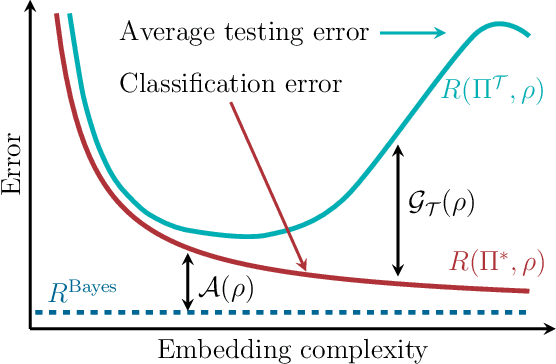
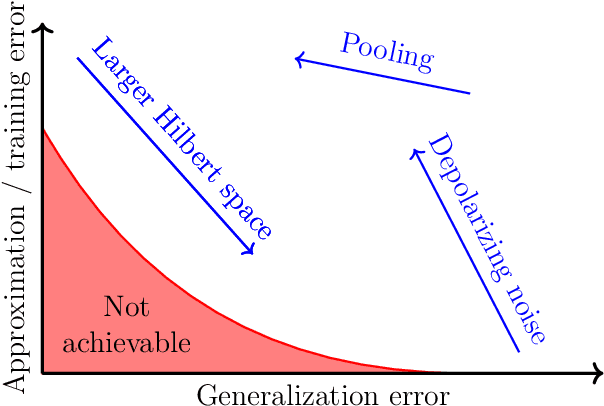
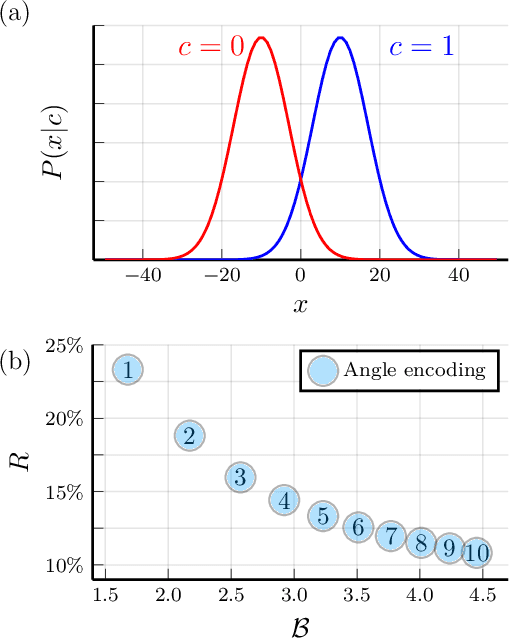
We study the machine learning problem of generalization when quantum operations are used to classify either classical data or quantum channels, where in both cases the task is to learn from data how to assign a certain class $c$ to inputs $x$ via measurements on a quantum state $\rho(x)$. A trained quantum model generalizes when it is able to predict the correct class for previously unseen data. We show that the accuracy and generalization capability of quantum classifiers depend on the (R\'enyi) mutual informations $I(C{:}Q)$ and $I_2(X{:}Q)$ between the quantum embedding $Q$ and the classical input space $X$ or class space $C$. Based on the above characterization, we then show how different properties of $Q$ affect classification accuracy and generalization, such as the dimension of the Hilbert space, the amount of noise, and the amount of neglected information via, e.g., pooling layers. Moreover, we introduce a quantum version of the Information Bottleneck principle that allows us to explore the various tradeoffs between accuracy and generalization.

Mixed State Entanglement Classification using Artificial Neural Networks

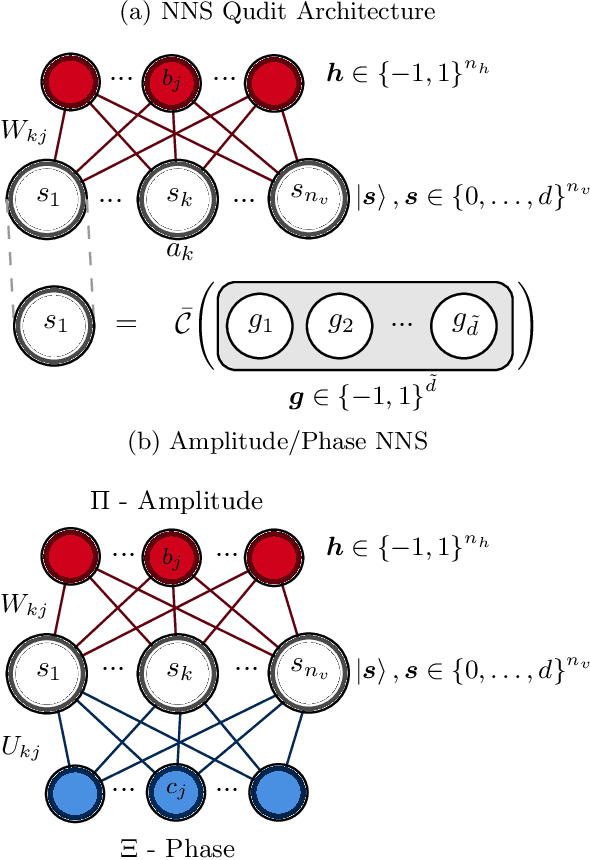
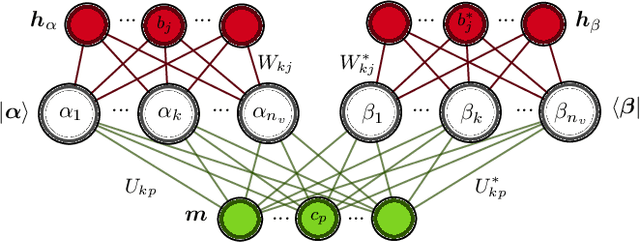
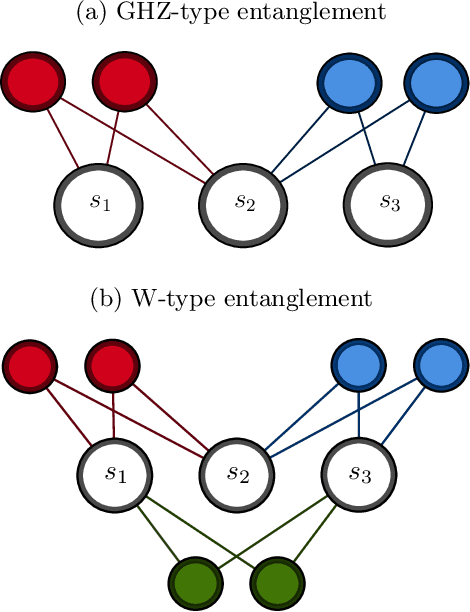
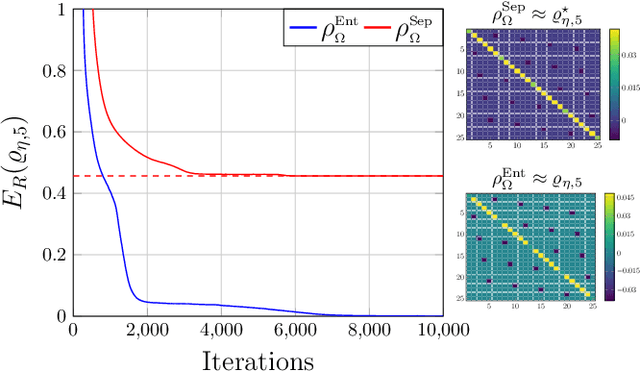
Reliable methods for the classification and quantification of quantum entanglement are fundamental to understanding its exploitation in quantum technologies. One such method, known as Separable Neural Network Quantum States (SNNS), employs a neural network inspired parameterisation of quantum states whose entanglement properties are explicitly programmable. Combined with generative machine learning methods, this ansatz allows for the study of very specific forms of entanglement which can be used to infer/measure entanglement properties of target quantum states. In this work, we extend the use of SNNS to mixed, multipartite states, providing a versatile and efficient tool for the investigation of intricately entangled quantum systems. We illustrate the effectiveness of our method through a number of examples, such as the computation of novel tripartite entanglement measures, and the approximation of ultimate upper bounds for qudit channel capacities.

Analytical Bounds for Dynamic Multi-Channel Discrimination

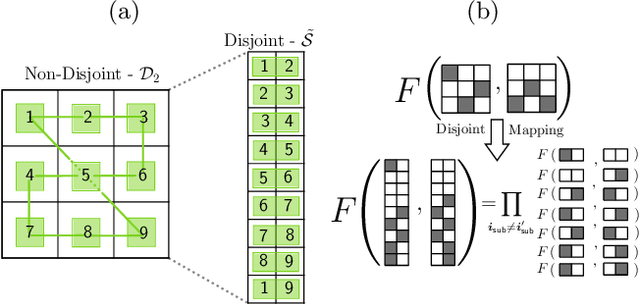
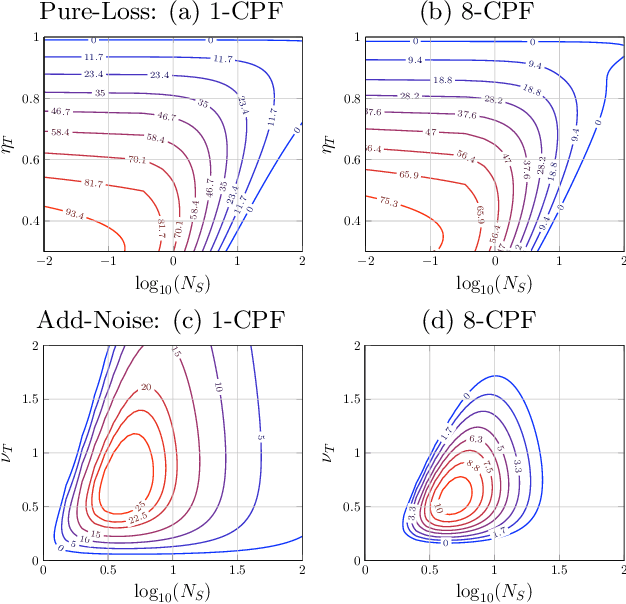
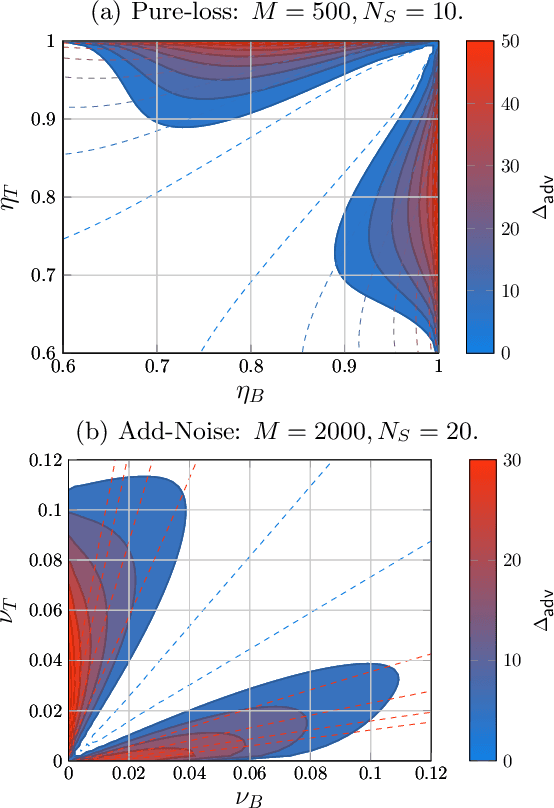
The ability to precisely discriminate multiple quantum channels is fundamental to achieving quantum enhancements in data-readout, target detection, pattern recognition, and more. Optimal discrimination protocols often rely on entanglement shared between an incident probe and a protected idler-mode. While these protocols can be highly advantageous over classical ones, the storage of idler-modes is extremely challenging in practice. In this work, we explicitly define idler-free protocols based on the use of multipartite entangled probe states. We show that using non-disjoint distributions of multipartite probe states over multi-channels can be described by dynamic discrimination protocols. Analytical bounds for their error probabilities are derived for arbitrary pattern size, revealing idler-free protocols that display performance close to idler-assistance for powerful, near-term quantum sensing applications.

Ultimate Limits of Thermal Imaging

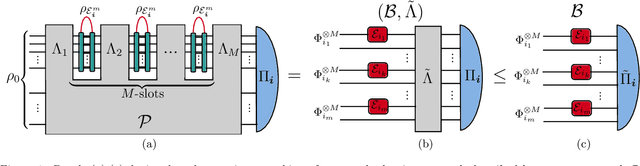
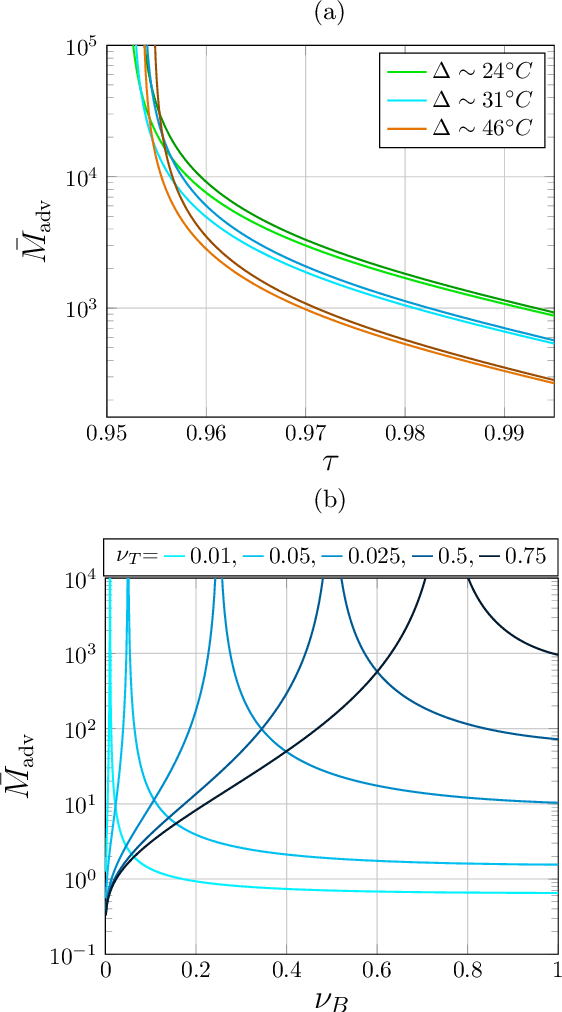
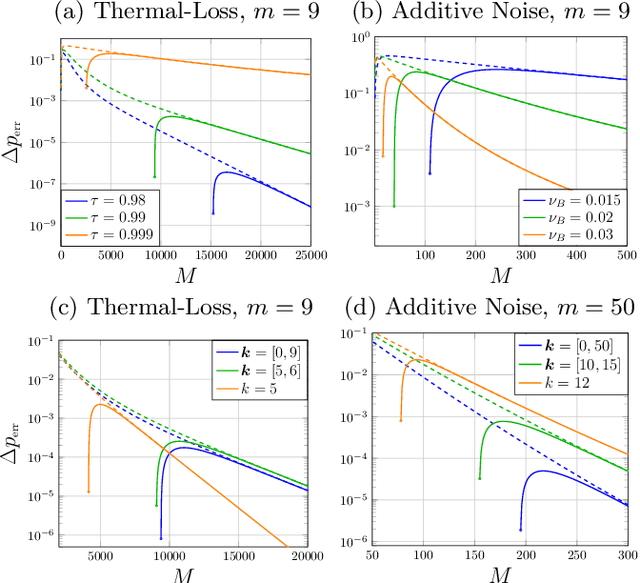
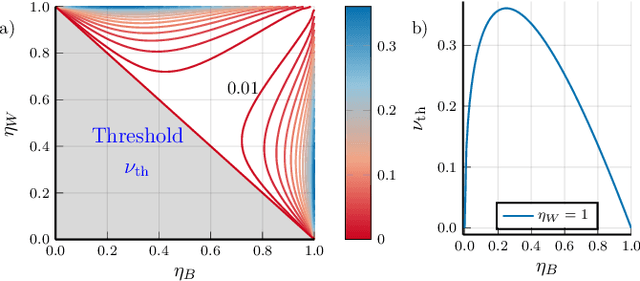
Quantum Channel Discrimination (QCD) presents a fundamental task in quantum information theory, with critical applications in quantum reading, illumination, data-readout and more. The extension to multiple quantum channel discrimination has seen a recent focus to characterise potential quantum advantage associated with quantum enhanced discriminatory protocols. In this paper, we study thermal imaging as an environment localisation task, in which thermal images are modelled as ensembles of Gaussian phase insensitive channels with identical transmissivity, and pixels possess properties according to background (cold) or target (warm) thermal channels. Via the teleportation stretching of adaptive quantum protocols, we derive ultimate limits on the precision of pattern classification of abstract, binary thermal image spaces, and show that quantum enhanced strategies may be used to provide significant quantum advantage over known optimal classical strategies. The environmental conditions and necessary resources for which advantage may be obtained are studied and discussed. We then numerically investigate the use of quantum enhanced statistical classifiers, in which quantum sensors are used in conjunction with machine learning image classification methods. Proving definitive advantage in the low loss regime, this work motivates the use of quantum enhanced sources for short-range thermal imaging and detection techniques for future quantum technologies.

Quantum-enhanced barcode decoding and pattern recognition

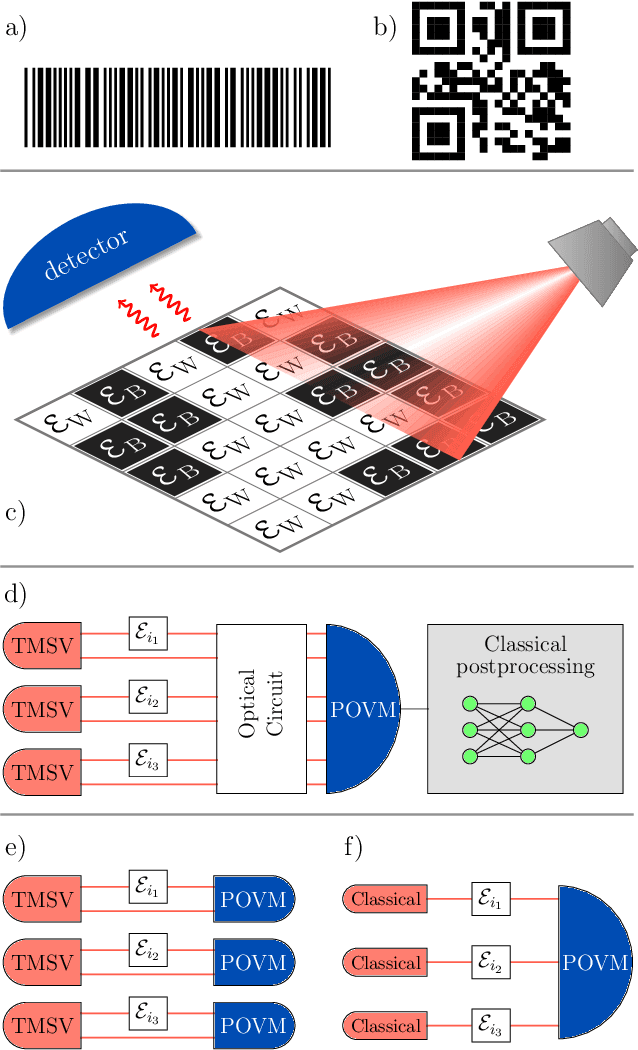
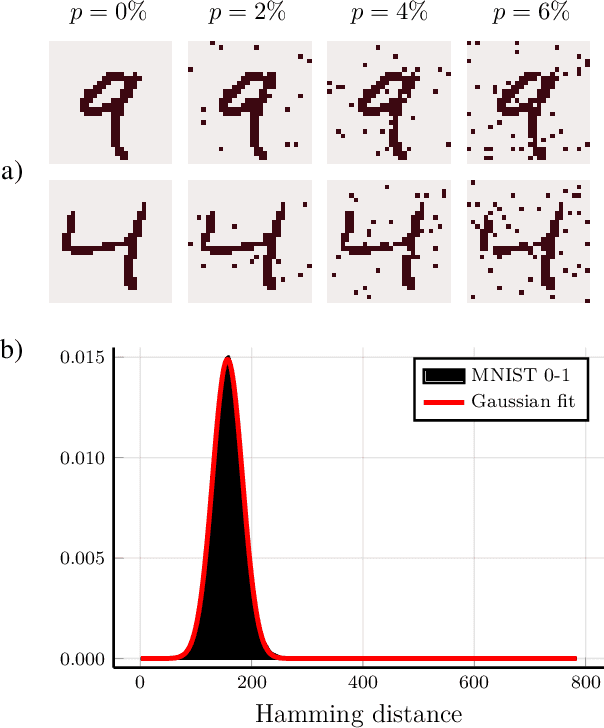
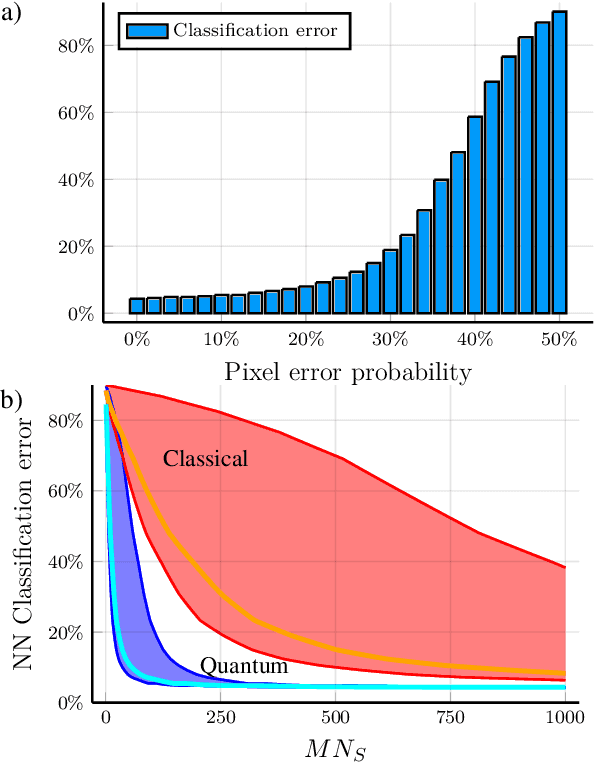
Quantum hypothesis testing is one of the most fundamental problems in quantum information theory, with crucial implications in areas like quantum sensing, where it has been used to prove quantum advantage in a series of binary photonic protocols, e.g., for target detection or memory cell readout. In this work, we generalize this theoretical model to the multi-partite setting of barcode decoding and pattern recognition. We start by defining a digital image as an array or grid of pixels, each pixel corresponding to an ensemble of quantum channels. Specializing each pixel to a black and white alphabet, we naturally define an optical model of barcode. In this scenario, we show that the use of quantum entangled sources, combined with suitable measurements and data processing, greatly outperforms classical coherent-state strategies for the tasks of barcode data decoding and classification of black and white patterns. Moreover, introducing relevant bounds, we show that the problem of pattern recognition is significantly simpler than barcode decoding, as long as the minimum Hamming distance between images from different classes is large enough. Finally, we theoretically demonstrate the advantage of using quantum sensors for pattern recognition with the nearest neighbor classifier, a supervised learning algorithm, and numerically verify this prediction for handwritten digit classification.

Noise-Assisted Variational Hybrid Quantum-Classical Optimization

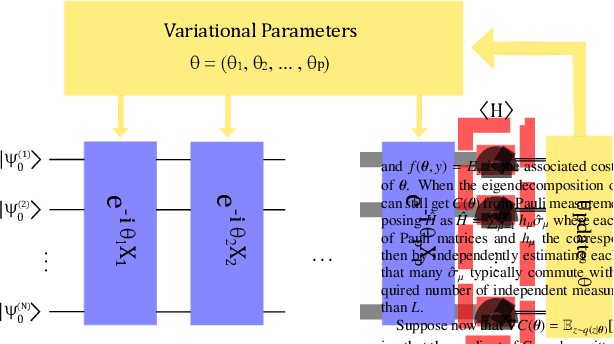
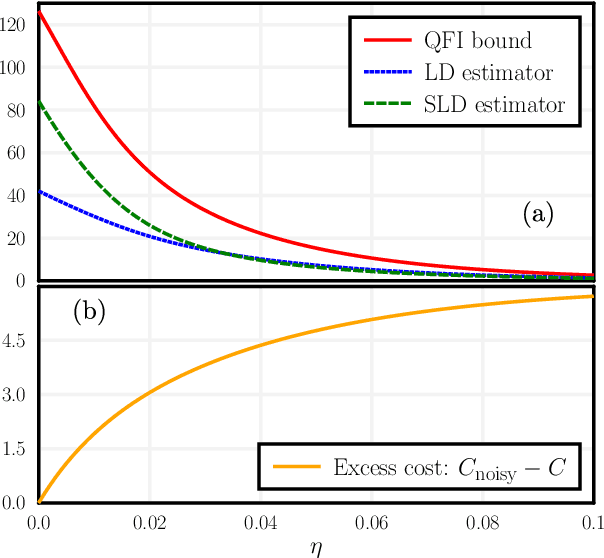
Variational hybrid quantum-classical optimization represents one the most promising avenue to show the advantage of nowadays noisy intermediate-scale quantum computers in solving hard problems, such as finding the minimum-energy state of a Hamiltonian or solving some machine-learning tasks. In these devices noise is unavoidable and impossible to error-correct, yet its role in the optimization process is not much understood, especially from the theoretical viewpoint. Here we consider a minimization problem with respect to a variational state, iteratively obtained via a parametric quantum circuit, taking into account both the role of noise and the stochastic nature of quantum measurement outcomes. We show that the accuracy of the result obtained for a fixed number of iterations is bounded by a quantity related to the Quantum Fisher Information of the variational state. Using this bound, we find the unexpected result that, in some regimes, noise can be beneficial, allowing a faster solution to the optimization problem.