Quantum-enhanced barcode decoding and pattern recognition
Paper and Code
Oct 07, 2020
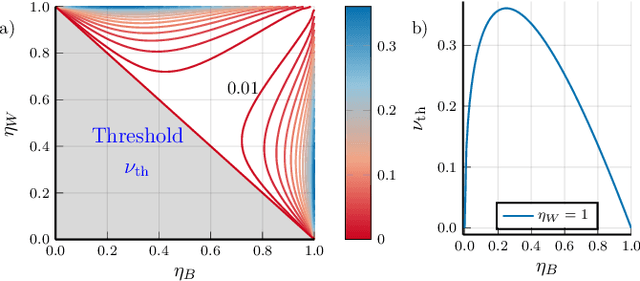
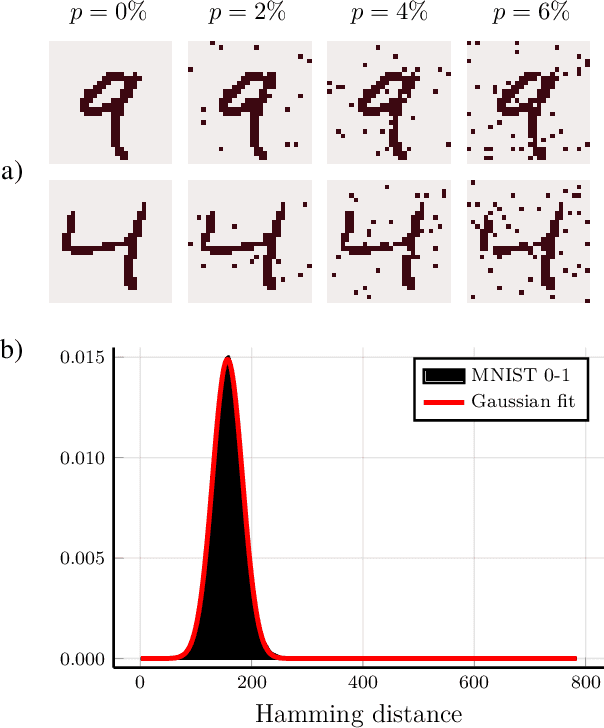
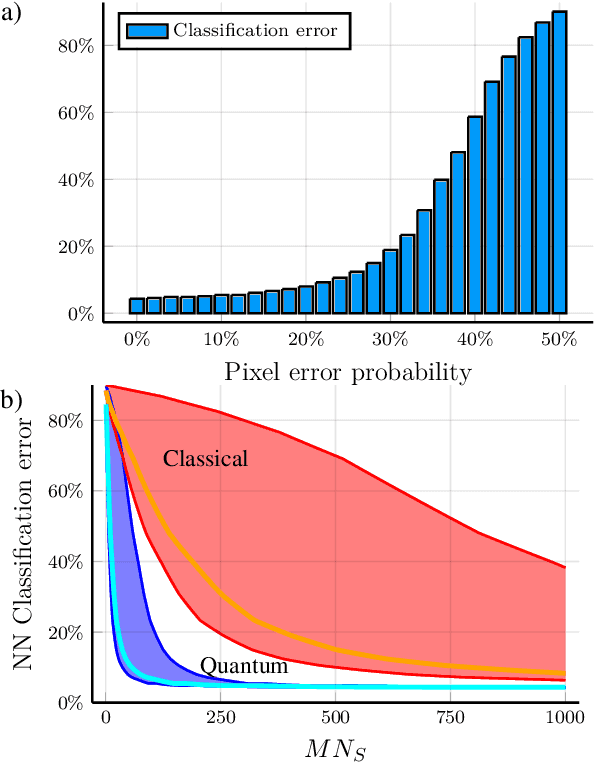
Quantum hypothesis testing is one of the most fundamental problems in quantum information theory, with crucial implications in areas like quantum sensing, where it has been used to prove quantum advantage in a series of binary photonic protocols, e.g., for target detection or memory cell readout. In this work, we generalize this theoretical model to the multi-partite setting of barcode decoding and pattern recognition. We start by defining a digital image as an array or grid of pixels, each pixel corresponding to an ensemble of quantum channels. Specializing each pixel to a black and white alphabet, we naturally define an optical model of barcode. In this scenario, we show that the use of quantum entangled sources, combined with suitable measurements and data processing, greatly outperforms classical coherent-state strategies for the tasks of barcode data decoding and classification of black and white patterns. Moreover, introducing relevant bounds, we show that the problem of pattern recognition is significantly simpler than barcode decoding, as long as the minimum Hamming distance between images from different classes is large enough. Finally, we theoretically demonstrate the advantage of using quantum sensors for pattern recognition with the nearest neighbor classifier, a supervised learning algorithm, and numerically verify this prediction for handwritten digit classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge