Learning to Classify Quantum Phases of Matter with a Few Measurements

We study the identification of quantum phases of matter, at zero temperature, when only part of the phase diagram is known in advance. Following a supervised learning approach, we show how to use our previous knowledge to construct an observable capable of classifying the phase even in the unknown region. By using a combination of classical and quantum techniques, such as tensor networks, kernel methods, generalization bounds, quantum algorithms, and shadow estimators, we show that, in some cases, the certification of new ground states can be obtained with a polynomial number of measurements. An important application of our findings is the classification of the phases of matter obtained in quantum simulators, e.g., cold atom experiments, capable of efficiently preparing ground states of complex many-particle systems and applying simple measurements, e.g., single qubit measurements, but unable to perform a universal set of gates.

Noise-Assisted Variational Hybrid Quantum-Classical Optimization

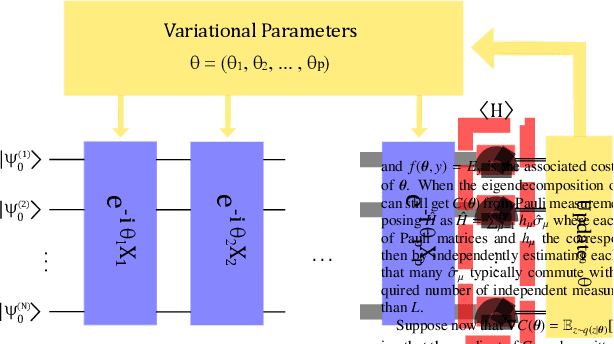
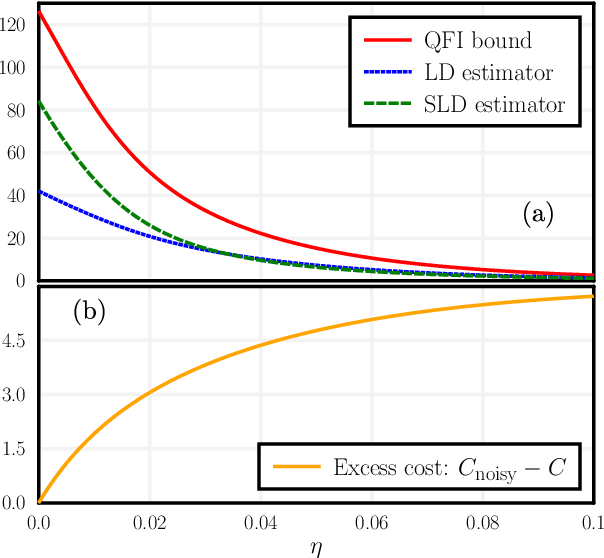
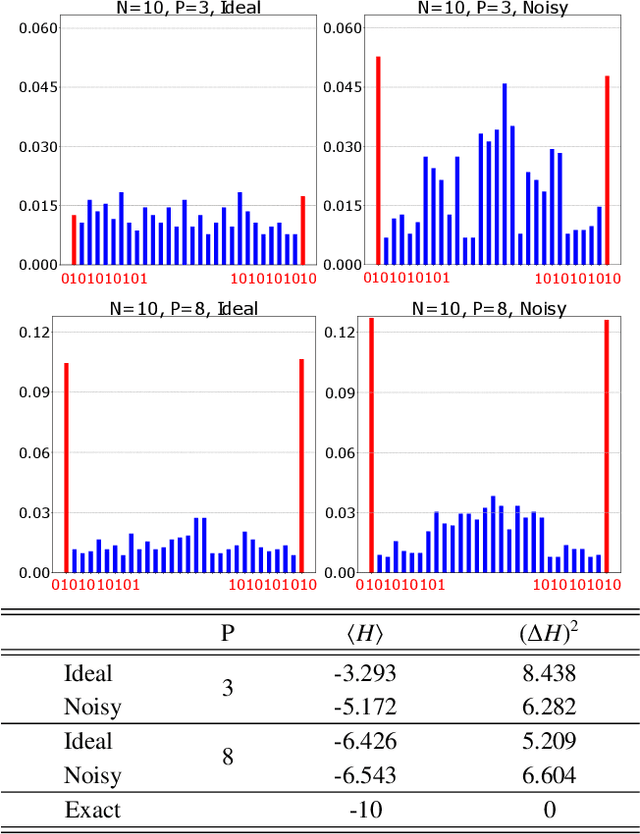
Variational hybrid quantum-classical optimization represents one the most promising avenue to show the advantage of nowadays noisy intermediate-scale quantum computers in solving hard problems, such as finding the minimum-energy state of a Hamiltonian or solving some machine-learning tasks. In these devices noise is unavoidable and impossible to error-correct, yet its role in the optimization process is not much understood, especially from the theoretical viewpoint. Here we consider a minimization problem with respect to a variational state, iteratively obtained via a parametric quantum circuit, taking into account both the role of noise and the stochastic nature of quantum measurement outcomes. We show that the accuracy of the result obtained for a fixed number of iterations is bounded by a quantity related to the Quantum Fisher Information of the variational state. Using this bound, we find the unexpected result that, in some regimes, noise can be beneficial, allowing a faster solution to the optimization problem.