Laura Gentini
Noise-Assisted Variational Hybrid Quantum-Classical Optimization
Dec 13, 2019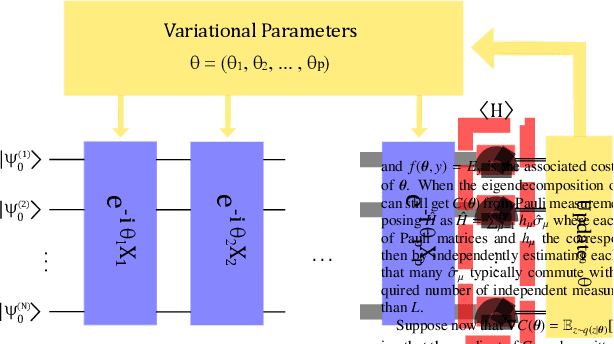
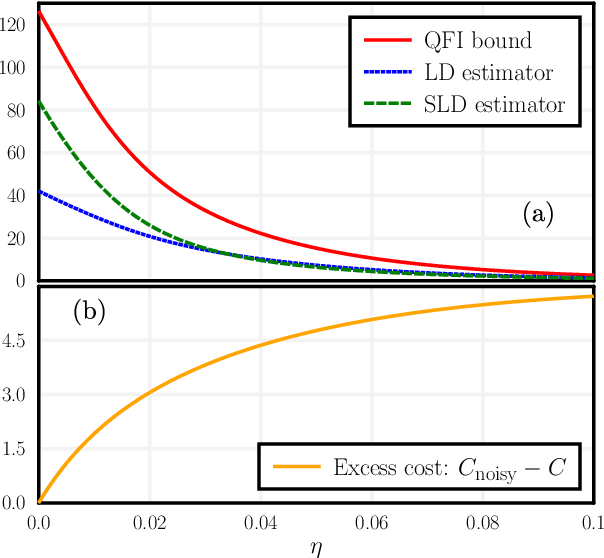
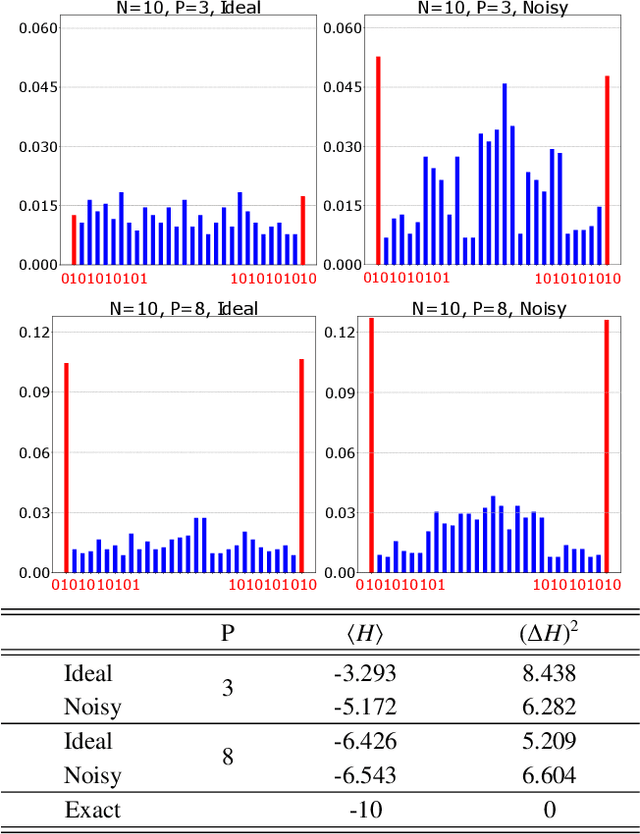
Abstract:Variational hybrid quantum-classical optimization represents one the most promising avenue to show the advantage of nowadays noisy intermediate-scale quantum computers in solving hard problems, such as finding the minimum-energy state of a Hamiltonian or solving some machine-learning tasks. In these devices noise is unavoidable and impossible to error-correct, yet its role in the optimization process is not much understood, especially from the theoretical viewpoint. Here we consider a minimization problem with respect to a variational state, iteratively obtained via a parametric quantum circuit, taking into account both the role of noise and the stochastic nature of quantum measurement outcomes. We show that the accuracy of the result obtained for a fixed number of iterations is bounded by a quantity related to the Quantum Fisher Information of the variational state. Using this bound, we find the unexpected result that, in some regimes, noise can be beneficial, allowing a faster solution to the optimization problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge