Generalization in Quantum Machine Learning: a Quantum Information Perspective
Paper and Code
Feb 17, 2021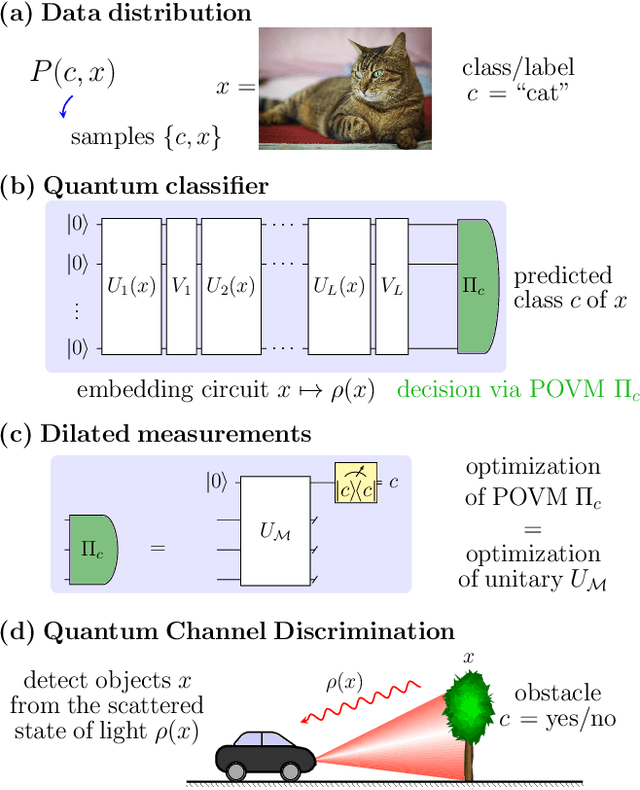
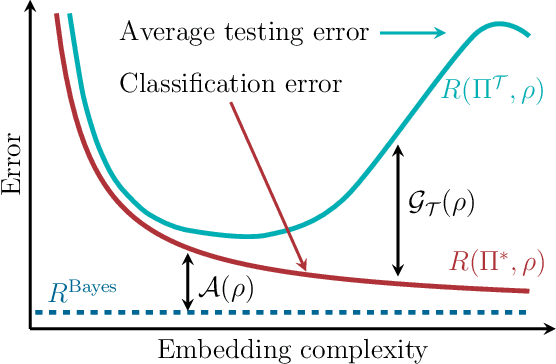
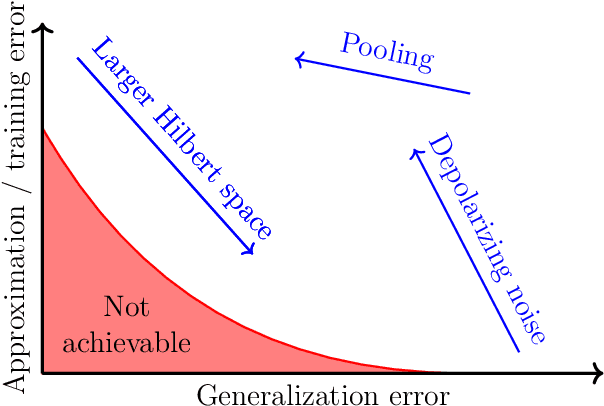
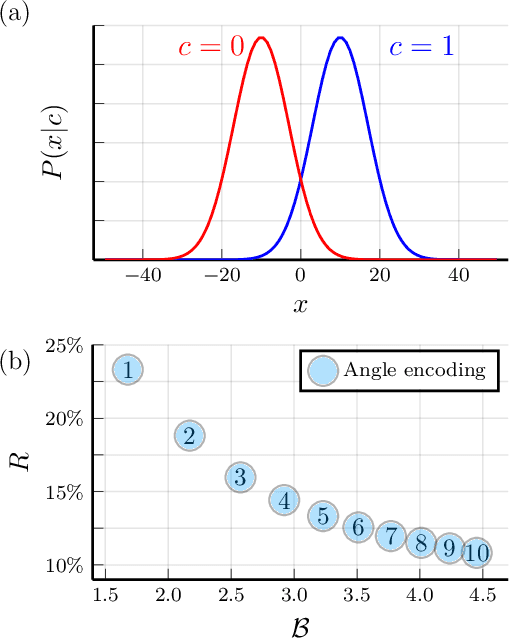
We study the machine learning problem of generalization when quantum operations are used to classify either classical data or quantum channels, where in both cases the task is to learn from data how to assign a certain class $c$ to inputs $x$ via measurements on a quantum state $\rho(x)$. A trained quantum model generalizes when it is able to predict the correct class for previously unseen data. We show that the accuracy and generalization capability of quantum classifiers depend on the (R\'enyi) mutual informations $I(C{:}Q)$ and $I_2(X{:}Q)$ between the quantum embedding $Q$ and the classical input space $X$ or class space $C$. Based on the above characterization, we then show how different properties of $Q$ affect classification accuracy and generalization, such as the dimension of the Hilbert space, the amount of noise, and the amount of neglected information via, e.g., pooling layers. Moreover, we introduce a quantum version of the Information Bottleneck principle that allows us to explore the various tradeoffs between accuracy and generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge